题目内容
(本题满分10分)
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.

(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
(1)平行四边形
(2)菱形
(3)菱形
(4)略
(本小题满分10分)
解:(1)四边形EGFH是平行四边形. …………………………1分
 证明:∵ ABCD的对角线AC、BD交于点O.
证明:∵ ABCD的对角线AC、BD交于点O.
 ∴点O是 ABCD的对称中心.
∴点O是 ABCD的对称中心.
∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形. …………………………4分
(2)菱形. …………………………5分
(3)菱形. …………………………6分
(4)四边形EGFH是正方形. …………………………7分

 证明:∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.
证明:∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.
 ∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.
∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.
∵EF⊥GH ,∴∠GOF=90°.∴∠BOG=∠COF.
∴△BOG≌△COF.∴OG=OF,∴GH=EF. …………………………9分
由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH.
∴四边形EGFH是正方形. …………………………10分
解:(1)四边形EGFH是平行四边形. …………………………1分
 证明:∵ ABCD的对角线AC、BD交于点O.
证明:∵ ABCD的对角线AC、BD交于点O. ∴点O是 ABCD的对称中心.
∴点O是 ABCD的对称中心.∴EO=FO,GO=HO.
∴四边形EGFH是平行四边形. …………………………4分
(2)菱形. …………………………5分
(3)菱形. …………………………6分
(4)四边形EGFH是正方形. …………………………7分

 证明:∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形.
证明:∵AC=BD,∴ ABCD是矩形. 又∵AC⊥BD, ∴ ABCD是菱形. ∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.
∴ ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°.OB=OC.∵EF⊥GH ,∴∠GOF=90°.∴∠BOG=∠COF.
∴△BOG≌△COF.∴OG=OF,∴GH=EF. …………………………9分
由(1)知四边形EGFH是平行四边形,又∵EF⊥GH,EF=GH.
∴四边形EGFH是正方形. …………………………10分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
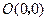 ,
,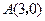 ,
,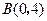 ,请你画出
,请你画出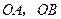 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形 ;
;
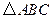 绕顶点
绕顶点 按顺时针方向旋转
按顺时针方向旋转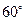 ,得到
,得到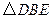 ,连结
,连结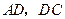 ,
,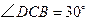 .求证:
.求证: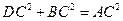 ,即四边形
,即四边形 是勾股四边形
是勾股四边形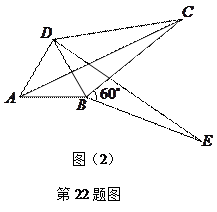
 是
是 对角线
对角线 上的两点,且
上的两点,且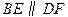 .
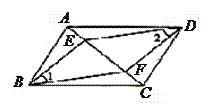
.
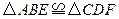 ;
;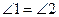 .
.
 、
、 上,
上, ^
^ ^
^ 、
、
 =
=
 =
=
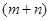 的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )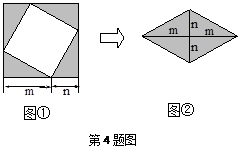



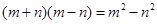

 -2
-2 -2
-2