题目内容
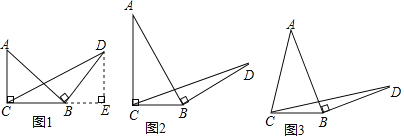
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过点A作AE//BC与过点D作CD的垂线交于点E.

(1)如图1,若CE交AD于点F,BC=6,∠B=30°,求AE的长;
(2)如图2,求证AE+CE=BC.
【答案】(1)2;(2)见详解.
【解析】
(1)由点D是AB中点,∠B=30°得到△ACD是等边三角形,由30°角所对直角边等于斜边的一半,得到AC=![]() ,由BC=6,即可得到AC=
,由BC=6,即可得到AC=![]() ,同理可计算得到
,同理可计算得到![]() ;
;
(2)延长ED,交BC于点G,可证△ADE≌△BDG,得到AE=BG,然后证明△CDE≌△CDG,得到CE=CG,然后即可得到AE+CE=BC.
解:(1)在Rt△ABC中,∠ACB=90°,D是AB的中点,
∴AD=BD=CD,
∵∠B=30°,
∴∠BCD=∠B=30°,∠BAC=60°
∴△ACD是等边三角形.
∴AC=AD=![]()
∵AE//BC,CD⊥DE,
∴∠CAE=∠ACB=90°,∠CDE=90°,
∴△ACE≌△DCE,
∴∠ACE=∠DCE=30°,
∴CE=2AE.
在Rt△ABC中,![]() ,BC=6,
,BC=6,
∴![]() ,
,
∴![]() ,
,
同理,在Rt△ACE中,![]()
解得:![]() ,
,
∴AE的长度为:2.
(2)如图,延长ED,交BC于点G,则
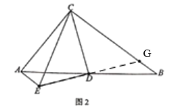
∵点D是AB的中点,
∴AD=BD,
∵AE∥BC,
∴∠EAD=∠GBD,
∵∠ADE=∠BDG,
∴△ADE≌△BDG(ASA),
∴AE=BG.DE=DG
∵CD⊥ED,
∴∠CDE=∠CDG=90°,
又CD=CD,
∴△CDE≌△CDG(SAS),
∴CE=CG,
∵BC=BG+CG,
∴BC=AE+EC.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目