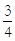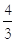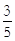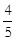题目内容
如图,在矩形ABCD中，对角线AC、BD相较于O,DE⊥AC于E，∠EDC∶∠EDA=1∶2，且AC=10，则DE的长度是 ．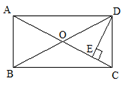
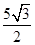
∵四边形ABCD是矩形，∴∠ADC=90°，AC=BD=10，OA=OC=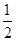
AC=5，OB=OD=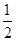BD=5，
∴OC=OD，∴∠ODC=∠OCD，∵∠EDC：∠EDA=1：2，∠EDC+∠EDA=90°，∴∠EDC=30°，∠EDA=60°，
∵DE⊥AC，∴∠DEC=90°，∴∠DCE=90°-∠EDC=60°，∴∠ODC=∠OCD=60°，∴∠ODC+∠OCD+∠DOC=180°，
∴∠COD=60°，∴△OCD是等边三角形，DE=sin60°•OD=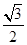
×5=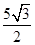
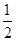AC=5，OB=OD=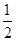BD=5，∴OC=OD，∴∠ODC=∠OCD，∵∠EDC：∠EDA=1：2，∠EDC+∠EDA=90°，∴∠EDC=30°，∠EDA=60°，
∵DE⊥AC，∴∠DEC=90°，∴∠DCE=90°-∠EDC=60°，∴∠ODC=∠OCD=60°，∴∠ODC+∠OCD+∠DOC=180°，
∴∠COD=60°，∴△OCD是等边三角形，DE=sin60°•OD=
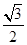×5=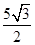
练习册系列答案
相关题目
的值是（▲）
．
，
，
分别垂直对角线
于
，
.
；
，
，求矩形
