Question

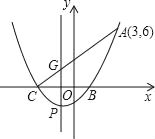
【题目】如图，一元二次方程x2+2x﹣3=0的两根x1，x2（x1＜x2）是抛物线y=ax2+bx+c与x轴的两个交点C，B的横坐标，且此抛物线过点A（3，6）．

（1）求此二次函数的解析式；

（2）设此抛物线的顶点为P，对称轴与线段AC相交于点G，则P点坐标为　 　，G点坐标为　 　；

（3）在x轴上有一动点M，当MG+MA取得最小值时，求点M的坐标．

Answer 1

【答案】（1）抛物线解析式为y=x2+x﹣；（2）抛物线顶点P的坐标为（﹣1，﹣2），G点坐标为（﹣1，2）；（3）M点坐标为（0，0）

【解析】

（1）可先根据一元二次方程求出x1，x2的坐标，也就求出了B，C两点的坐标，然后可用交点式的二次函数通式来设二次函数的解析式，根据已知的A点的坐标求出二次函数的解析式．
（2）根据（1）二次函数解析式可得出顶点P的坐标和对称轴的解析式，G点就是直线AC与抛物线对称轴的交点，可先根据A，C的坐标，用待定系数法求出AC所在直线的解析式，然后将P点的横坐标代入求得的一次函数的解析式中即可求出G的坐标．
（3）本题的关键是先确定M点的位置，可先做A关于x轴的对称点A′然后连接A′C，与x轴的交点就是点M，那么可根据A′，C两点的坐标求出A′C所在直线的解析式，又已知了M在x轴上即可求出M点的坐标．

解：（1）解方程x2+2x﹣3=0

得x1=﹣3，x2=1．

∴抛物线与x轴的两个交点坐标为：C（﹣3，0），B（1，0），

设抛物线的解析式为y=a（x+3）（x﹣1）．

∵A（3，6）在抛物线上，

∴6=a（3+3）（3﹣1），

∴a=，

∴抛物线解析式为y=x2+x﹣．

（2）由y=x2+x﹣=（x+1）2﹣2，

∴抛物线顶点P的坐标为（﹣1，﹣2），对称轴方程为x=﹣1．

设直线AC的解析式为y=kx+b，

∵A（3，6），C（﹣3，0）在该直线上，

∴ ,

解得：k=1,b=3,

∴直线AC的解析式为：y=x+3．

将x=﹣1代入y=x+3

得y=2，

∴G点坐标为（﹣1，2）．

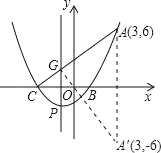
（3）作A关于x轴的对称点A′（3，﹣6），

连接A′G，A′G与x轴交于点M即为所求的点．

设直线A′G的解析式为y=kx+b．

∴ ，解得： ，

∴直线A′G的解析式为y=﹣2x，令x=0，则y=0．

∴M点坐标为（0，0）．