题目内容
正六边形的各边中点连起来形成新正六边形，其面积是原正六边形面积的分析：根据正六边形的性质，求出原正六边形的边长与新正六边形的边长的关系，然后根据相似多边形的面积的比等于相似比的平方进行求解即可．
解答：
解：如图，设原正六边形的边长为a，
则新正六边形的边长为，a•sin60°=
a，
∴新正六边形的面积：原正六边形的面积=（
a：a）2=
，
∴其面积是原正六边形面积的
倍．
故答案为：
．
解：如图，设原正六边形的边长为a，则新正六边形的边长为，a•sin60°=
| ||
| 2 |
∴新正六边形的面积：原正六边形的面积=（
| ||
| 2 |
| 3 |
| 4 |
∴其面积是原正六边形面积的
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题主要考查了相似多边形的面积的比等于相似比的性质，求出两正六边形的边长的比是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
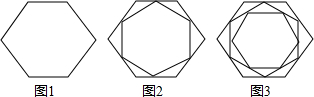如图，图1是一个正六边形，分别连接这个正六边形各边中点得到图2，再分别连接图2内小正六边形各边中点得到图3．
