题目内容
四边形ABCD各角的比为∠A：∠B：∠C：∠D=1：2：3：4，则这个四边形为 ．
考点：多边形内角与外角
专题：
分析：设四个角的度数分别为：X，2X，3X，4X，根据四边形的内角和公式即可求得各角的度数，从而便可求得该四边形的形状．
解答：解：由题意，设∠A、∠B、∠C、∠D的度数分别为X、2X、3X、4X，
由四边形的内角和为360°，得X+2X+3X+4X=360°，
解得X=36°，
∴∠A=36°，∠B=72°，∠C=108°，∠D=144°，
∠A+∠C=∠B+∠D=180°，
对角互补，所以四边形是圆内接四边形．
故答案为：圆内接四边形．
由四边形的内角和为360°，得X+2X+3X+4X=360°，
解得X=36°，
∴∠A=36°，∠B=72°，∠C=108°，∠D=144°，
∠A+∠C=∠B+∠D=180°，
对角互补，所以四边形是圆内接四边形．
故答案为：圆内接四边形．
点评：此题考查四边形的判定，通过设适当的参数，根据四边形的内角和建立方程，求得各角的度数进行判定．
练习册系列答案
相关题目
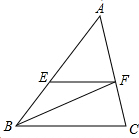如图，在△ABC中，E、F分别是AB、AC上两点，EF∥BC，BF平分∠ABC，若∠BFE=35°，则∠AEF的度数为
如图，小明从点A出发，沿直线前进20m后向左转30°，再沿直线前进20m，又向左转30°…照这样走下去，小明第一次回到出发点A，一共走了三角形的两边长分别为a、b且a＜b，则周长l的取值范围是（ ）
| A、3a＜l＜3b |
| B、2b＜l＜2a+2b |
| C、2a+b＜l＜3b |
| D、无法确定 |