题目内容
在平面直角坐标系中,已知点A(4,0),点B(0,3).点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发.(1)连接AQ,当△ABQ是直角三角形时,求点Q的坐标;
(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时∠AQP的度数;
(3)过点A作AC⊥AB,AC交射线PQ于点C,连接BC,D是BC的中点.在点P、Q的运动过程中,是否存在某时刻,使得以A、C、Q、D为顶点的四边形是平行四边形,若存在,试求出这时tan∠ABC的值;若不存在,试说明理由.
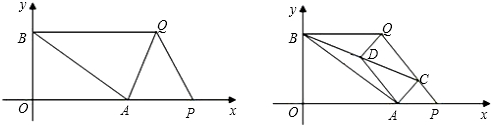
分析:(1)由于∠ABQ<90°,若△ABQ是直角三角形,需要考虑两种情况:
①∠BAQ=90°,此时△BAQ∽△ABO,根据相似三角形所得比例线段,可求出BQ的长,即可得到Q点坐标;
②∠BQA=90°,此时四边形BOAQ是矩形,BQ=OA,由此可求出Q点坐标.
(2)假设P点翻折到AB上时,落点为E,那么∠QAP=∠QAE,QE=QP;由于BQ∥OP,那么∠QAP=∠BQA=∠BAQ,即BQ=BA=5,此时P、Q运动了2.5s,所以AP=AE=
,即E是AB的中点;分别过E、Q作BQ、OP的垂线,设垂足为F、H,易求EF=PH=
,即可证得△QPH≌△QEF,得∠EQF=∠PQH,由此发现∠EQP=90°,而∠PQA=∠EQA,由此可求得∠AQP的度数.
(3)假设存在这样的平行四边形,可分作两种情况考虑:
①点C在线段PQ上,可延长AC、BQ交于点F,由于DQ∥AC,因此DQ是△BCF的中位线,则FC=2DQ=2AC,过F作FH⊥x轴于H,由于∠BAC=90°,可证得△AOB∽△FHA,通过得到的比例线段,即可求出AF的长,进而可得到AC的长;在Rt△BAC中,已知了AC、BA的长,即可求出∠ABC的正切值;
②点C在PQ的延长线上,设AD、AC与BQ的交点分别为G、F,按照①的思路可证得AD=CQ=2AG,那么在相似三角形△CFQ和△AFG中,FC=2AF,即AC=3AF,AF的长在①中已求得,由此可得到AC的长,进而可求出∠ABC的正切值.
①∠BAQ=90°,此时△BAQ∽△ABO,根据相似三角形所得比例线段,可求出BQ的长,即可得到Q点坐标;
②∠BQA=90°,此时四边形BOAQ是矩形,BQ=OA,由此可求出Q点坐标.
(2)假设P点翻折到AB上时,落点为E,那么∠QAP=∠QAE,QE=QP;由于BQ∥OP,那么∠QAP=∠BQA=∠BAQ,即BQ=BA=5,此时P、Q运动了2.5s,所以AP=AE=
| 5 |
| 2 |
| 3 |
| 2 |
(3)假设存在这样的平行四边形,可分作两种情况考虑:
①点C在线段PQ上,可延长AC、BQ交于点F,由于DQ∥AC,因此DQ是△BCF的中位线,则FC=2DQ=2AC,过F作FH⊥x轴于H,由于∠BAC=90°,可证得△AOB∽△FHA,通过得到的比例线段,即可求出AF的长,进而可得到AC的长;在Rt△BAC中,已知了AC、BA的长,即可求出∠ABC的正切值;
②点C在PQ的延长线上,设AD、AC与BQ的交点分别为G、F,按照①的思路可证得AD=CQ=2AG,那么在相似三角形△CFQ和△AFG中,FC=2AF,即AC=3AF,AF的长在①中已求得,由此可得到AC的长,进而可求出∠ABC的正切值.
解答: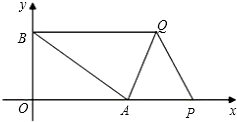 解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.
解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.
ⅰ)当∠BAQ=90°时,△AOB∽△BAQ,
∴
=
.解得BQ=
;
ⅱ)当∠BQA=90°时,BQ=OA=4,
∴Q(
,3)或Q(4,3).(4分)
(2)令点P翻折后落在线段AB上的点E处,
则∠EAQ=∠PAQ,∠EQA=∠PQA,AE=AP,QE=QP;
又BQ∥OP,
∴∠PAQ=∠BQA,∴∠EAQ=∠BQA,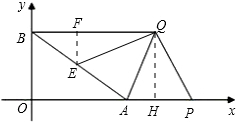
即AB=QB=5.
∴AP=
BQ=
,
∴AE=AP=
=
AB,即点E是AB的中点.
过点E作EF⊥BQ,垂足为点F,过点Q作QH⊥OP,垂足为点H,
则EF=
,PH=
,∴EF=PH.
又EQ=PQ,∠EFQ=∠PHQ=90°,
∴△EQF≌△PQH
∴∠EQF=∠PQH,从而∠PQE=90°.
∴∠AQP=∠AQE=45°.(8分)
(3)当点C在线段PQ上时,延长BQ与AC的延长线交于点F,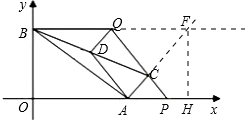
∵AC⊥AB,
∴△AOB∽△FHA.
∴
=
即
=
,
∴FA=
.
∵DQ∥AC,DQ=AC,且D为BC中点,
∴FC=2DQ=2AC.
∴AC=
.
在Rt△BAC中,tan∠ABC=
;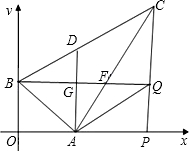
当点C在PQ的延长线上时,记BQ与AC的交点为F,记AD与BQ的交点为G,
∵CQ∥AD,CQ=AD且D为BC中点,
∴AD=CQ=2DG.
∴CQ=2AG=2PQ.
即:CQ:QP=2:1
又∵BQ∥OP
∴CF:AF=CQ:QP=2:1
∴FC=2AF,
又∵FA=
,
∴FC=
,
∴AC=
.
在Rt△BAC中,tan∠ABC=
.(12分)
 解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.
解:(1)根据题意,可得:A(4,0)、B(0,3),AB=5.ⅰ)当∠BAQ=90°时,△AOB∽△BAQ,
∴
| BQ |
| AB |
| AB |
| AO |
| 25 |
| 4 |
ⅱ)当∠BQA=90°时,BQ=OA=4,
∴Q(
| 25 |
| 4 |
(2)令点P翻折后落在线段AB上的点E处,
则∠EAQ=∠PAQ,∠EQA=∠PQA,AE=AP,QE=QP;
又BQ∥OP,
∴∠PAQ=∠BQA,∴∠EAQ=∠BQA,

即AB=QB=5.
∴AP=
| 1 |
| 2 |
| 5 |
| 2 |
∴AE=AP=
| 5 |
| 2 |
| 1 |
| 2 |
过点E作EF⊥BQ,垂足为点F,过点Q作QH⊥OP,垂足为点H,
则EF=
| 3 |
| 2 |
| 3 |
| 2 |
又EQ=PQ,∠EFQ=∠PHQ=90°,
∴△EQF≌△PQH
∴∠EQF=∠PQH,从而∠PQE=90°.
∴∠AQP=∠AQE=45°.(8分)
(3)当点C在线段PQ上时,延长BQ与AC的延长线交于点F,

∵AC⊥AB,
∴△AOB∽△FHA.
∴
| AB |
| FA |
| AO |
| FH |
| 5 |
| FA |
| 4 |
| 3 |
∴FA=
| 15 |
| 4 |
∵DQ∥AC,DQ=AC,且D为BC中点,
∴FC=2DQ=2AC.
∴AC=
| 5 |
| 4 |
在Rt△BAC中,tan∠ABC=
| 1 |
| 4 |

当点C在PQ的延长线上时,记BQ与AC的交点为F,记AD与BQ的交点为G,
∵CQ∥AD,CQ=AD且D为BC中点,
∴AD=CQ=2DG.
∴CQ=2AG=2PQ.
即:CQ:QP=2:1
又∵BQ∥OP
∴CF:AF=CQ:QP=2:1
∴FC=2AF,
又∵FA=
| 15 |
| 4 |
∴FC=
| 15 |
| 2 |
∴AC=
| 45 |
| 4 |
在Rt△BAC中,tan∠ABC=
| 9 |
| 4 |
点评:此题考查的知识点较多,涉及到图形的翻折变换、相似三角形及全等三角形的判定和性质、三角形中位线定理以及锐角三角函数的定义等知识,同时还考查了分类讨论的数学思想,难度较大.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB= 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.