题目内容
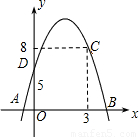
如图,已知抛物y=-x2+bx+c过点C(3,8),与x轴交于A,B两点,与y轴交于点D(0,5).(1)求该二次函数的关系式;
(2)求该抛物线的顶点M的坐标,并求四边形ABMD的面积.
【答案】分析:(1)将C(3,8),D(0,5)两点坐标代入y=-x2+bx+c中求b、c即可;
(2)由二次函数解析式求M点坐标,根据S四边形ABMD=S△ADO+S梯形ODMN+S△MNB求面积.
解答: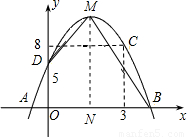 解:(1)根据题意,得C=5
解:(1)根据题意,得C=5
-9+3b+c=8(2分)
∴b=4,c=5.(3分)
∴这个二次函数的关系式为:y=-x2+4x+5;
(2)y=-x2+4x+5的顶点坐标为M(2,9),
令y=0,-x2+4x+5=0得x1=5,x2=-1,
A(-1,0)B(5,0),
∴S四边形ABMD=S△ADO+S梯形ODMN+S△MNB
= +
+ +
+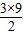 =30.
=30.
点评:本题考查了二次函数解析式的求法,坐标系中求图形的面积.关键是根据已知点的坐标,将四边形分割为两个三角形与一个梯形的面积和.
(2)由二次函数解析式求M点坐标,根据S四边形ABMD=S△ADO+S梯形ODMN+S△MNB求面积.
解答:
 解:(1)根据题意,得C=5
解:(1)根据题意,得C=5-9+3b+c=8(2分)
∴b=4,c=5.(3分)
∴这个二次函数的关系式为:y=-x2+4x+5;
(2)y=-x2+4x+5的顶点坐标为M(2,9),
令y=0,-x2+4x+5=0得x1=5,x2=-1,
A(-1,0)B(5,0),
∴S四边形ABMD=S△ADO+S梯形ODMN+S△MNB
=
 +
+ +
+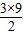 =30.
=30.点评:本题考查了二次函数解析式的求法,坐标系中求图形的面积.关键是根据已知点的坐标,将四边形分割为两个三角形与一个梯形的面积和.

练习册系列答案
相关题目
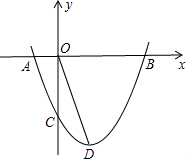 如图,已知抛物y=ax2+bx+c线经过A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物y=ax2+bx+c线经过A(-1,0)、B(3,0)、C(0,-3).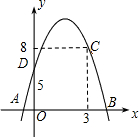 如图,已知抛物y=-x2+bx+c过点C(3,8),与x轴交于A,B两点,与y轴交于点D(0,5).
如图,已知抛物y=-x2+bx+c过点C(3,8),与x轴交于A,B两点,与y轴交于点D(0,5). 如图,已知抛物y=ax2+bx+c线经过A(-1,0)、B(3,0)、C(0,-3).
如图,已知抛物y=ax2+bx+c线经过A(-1,0)、B(3,0)、C(0,-3).