题目内容
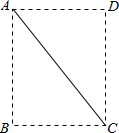 如图ABCD是矩形纸片,AC是对角线,把三角形ABC沿AC翻折,点B落到点E处,连接DE
如图ABCD是矩形纸片,AC是对角线,把三角形ABC沿AC翻折,点B落到点E处,连接DE(1)请根据题意补全图形;
(2)试判断四边形ACED的形状,并说明理由.
分析:过D作DF⊥AC于F,过E作EH⊥AC于H,根据矩形的性质得Rt△ABC≌Rt△CDA,再由折叠的性质得Rt△ABC≌Rt△AEC,则CE=CB=DA,CE与DA不平行,再根据全等三角形面积相等,可得DF=HE,又DF∥EH,可得四边形DFHE是平行四边形,于是有DE∥AC,即可判断四边形ACED是等腰梯形.
解答: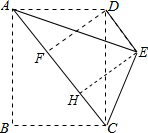 解:(1)如图所示;
解:(1)如图所示;
(2)四边形DACE是等腰梯形;
过D作DF⊥AC于F,过E作EH⊥AC于H,如图,
∵四边形ABCD为矩形,
∴Rt△ABC≌Rt△CDA,
又∵矩形沿着直线AC折叠,使点B落在点E处,
∴Rt△ABC≌Rt△AEC,
∴△ADC≌△CEA,
∴CE=AD,
根据全等三角形的面积相等,得:DF=EH,
∵EH∥DF,
∴四边形DFHE是平行四边形,
∴DE∥AC,
∵AD=CE,
∴四边形DACE是等腰梯形.
 解:(1)如图所示;
解:(1)如图所示;(2)四边形DACE是等腰梯形;
过D作DF⊥AC于F,过E作EH⊥AC于H,如图,
∵四边形ABCD为矩形,
∴Rt△ABC≌Rt△CDA,
又∵矩形沿着直线AC折叠,使点B落在点E处,
∴Rt△ABC≌Rt△AEC,
∴△ADC≌△CEA,
∴CE=AD,
根据全等三角形的面积相等,得:DF=EH,
∵EH∥DF,
∴四边形DFHE是平行四边形,
∴DE∥AC,
∵AD=CE,
∴四边形DACE是等腰梯形.
点评:本题考查了折叠的性质:折叠前后两图形全等,即对应角相等,对应线段相等.也考查了等腰梯形的判定与性质和矩形的性质.

练习册系列答案
相关题目
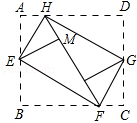 如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是
如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是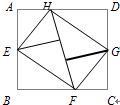 18、如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是( )
18、如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是( )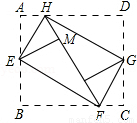 (2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.
(2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.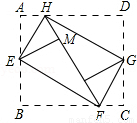 (2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.
(2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.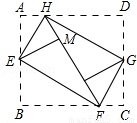 (2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.
(2008•宁德)如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是 厘米.