题目内容
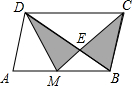 如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为
如图所示,已知M是平行四边形ABCD的AB边的中点,CM交BD于点E,BD=3BE,则图中阴影部分面积与平行四边形ABCD面积之比为分析:根据面积计算公式,找到底边及高之间的关系即可求解,过点A、M向BD作高,根据线段间的关系求解.
解答: 解:如图作AG⊥BD、MH⊥BD,垂足为G、H,
解:如图作AG⊥BD、MH⊥BD,垂足为G、H,
∵BD=3BE,C到BD的距离为△BEC和△BCD的高,
∴△BEC和△BCD的面积之比为1:3,
∵AG⊥BD、MH⊥BD,
∴AG∥MH,
∴
=
=
,
∵BD=3BE,
∴△DME和△ABD的面积之比为1:3,
∴阴影部分面积与平行四边形ABCD面积之比为1:3.
故答案为1:3.
 解:如图作AG⊥BD、MH⊥BD,垂足为G、H,
解:如图作AG⊥BD、MH⊥BD,垂足为G、H,∵BD=3BE,C到BD的距离为△BEC和△BCD的高,
∴△BEC和△BCD的面积之比为1:3,
∵AG⊥BD、MH⊥BD,
∴AG∥MH,
∴
| MH |
| AG |
| BM |
| BA |
| 1 |
| 2 |
∵BD=3BE,
∴△DME和△ABD的面积之比为1:3,
∴阴影部分面积与平行四边形ABCD面积之比为1:3.
故答案为1:3.
点评:本题考查了平行四边形的性质,求看似不相关的区域的两个面积之比,只要找到与两者都有关系的区域面积,根据彼此之间的关系即可求解.

练习册系列答案
相关题目
 14、已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( )
14、已知,AB是⊙O的直径,且C是圆上一点,小聪透过平举的放大镜从正上方看到水平桌面上的三角形图案的∠B(如图所示),那么下列关于∠A与放大镜中的∠B关系描述正确的是( ) 某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南北两楼相隔仅有20m(如图所示),试求:
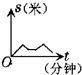
某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°,如果南北两楼相隔仅有20m(如图所示),试求: 小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的( )
小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的( )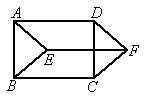
 小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的
小明同学骑自行车在上学的路上要经过两座山梁,行走的路线如图所示.已知上山的速度为v1米/分钟,平路的速度为v2米/分钟,下山的速度为v3米/分钟,其中v1<v2<v3.那么,小明同学上学骑自行车行走的路程S(米)与所用的时间t(分钟)的函数关系,可能是下面图象中的