题目内容
【题目】如图所示，
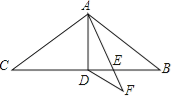
将若干个点摆成三角形图案，每条边（包括两个端点）有n（n是正整数且n＞1）个点，相应的图案中总的点数记为an ， 则 
+ 
+…+ 
=（ ）
A.
B.
C.
D.
【答案】B
【解析】解：每个边上有n个点，把每个边上的点数相加得3n，这样角上的点数被重复计算了一次，
故第n个图形的点数为3n﹣3，即an=3n﹣3，
令Sn= 
+ 
+…+ 
= 
+ 
+…+ 
= 
，
∴ + +…+ 
= + +…+ 
=1﹣ 
+ ﹣ 
+…+ 
﹣ 
= 
，
故选：B．
根据图象规律得出通项公式an=3n﹣3，根据数列{ }的特点即可用列项法求其前n项和的公式，而 + +…+ 是前2016项的和，代入前n项和公式即可得答案．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校为更好地培养学生兴趣，开展“拓展课程走班选课”活动，随机抽查了部分学生，了解他们最喜爱的项目类型（分为书法、围棋、戏剧、国画共4类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图． 最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
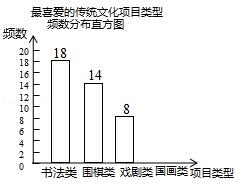
根据以上信息完成下列问题：
（1）频数分布表中a= ， b=；
（2）补全频数分布直方图；
（3）若全校共有学生1500名，估计该校最喜爱围棋的学生大约有多少人？
