Question

【题目】新知学习，若一条线段把一个平面图形分成面积相等的两部分，我们把这条段线做该平面图形的二分线解决问题:

（1）①三角形的中线、高线、角平分线中，一定是三角形的二分线的是_______

②如图1，已知△ABC中，AD是BC边上的中线，点E，F分别在AB，DC上，连接EF，与AD交于点G，若则EF_____(填“是”或“不是”)△ABC的一条二分线.并说明理由.

(2)如图2，四边形ABCD中，CD平行于AB，点G是AD的中点，射线CG交射线BA于点E，取EB的中点F，连接CF.求证:CF是四边形ABCD的二分线.

Answer 1

【答案】（1）①中线②是（2）证明见解析

【解析】

（1）①由平面图形的二分线定义可求解；

②由面积的和差关系可得S△BEF=S△ABD=S△ABC，可得EF是△ABC的一条二分线；

（2）根据EB的中点F，所以S△CBF=S△CEF，由AB∥DC，G是AD的中点，证明△CDG≌△EAG，所以S四边形AFCD=S△CEF，所以S四边形AFCD=S△CBF，可得CF是四边形ABCD的二分线；

解：（1）①三角形的中线、高线、角平分线中，一定是三角形的二分线的是中线，

故答案为：中线；.

②∵AD是BC边上的中线，

∴S△ABD=S△ACD,

又∵，

∴S四边形BEGD=S四边形AGFC，

∴S四边形BEGD+=S四边形AGFC+，

∴=S四边形AEFC，

所以EF是△ABC的一条二分线，

故答案为：是；

（2）如图：

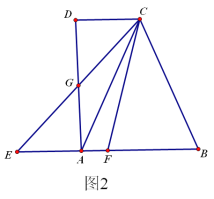
∵点G是AD的中点，

∴GD=AG，

∵AB∥DC，

∴∠D=∠GAE，

在△CDG和△EAG中，

，

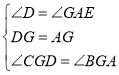∴△CDG≌△EAG（ASA），

∴S△CDG=S△EAG，

∵点F是EB的中点，

∴S△CFE=S△CBF，

即S△AGE+S四边形AGCF=S△CBF，

∴S△CDG+S四边形AGCF=S△CBF，即S四边形ADCF=S△CBF，

∴CF是四边形ABCD的二分线；