题目内容
【题目】动手操作: 如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题: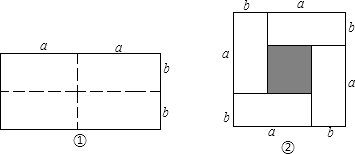
(1)观察图②,请用两种不同的方法表示阴影部分的面积;
(2)请写出三个代数式(a+b)2 , (a﹣b)2 , ab之间的一个等量关系. 问题解决:
根据上述(2)中得到的等量关系,解决下列问题:
已知:x+y=6,xy=3.求:(x﹣y)2的值.
【答案】
(1)解:(a+b)2﹣4ab或(a﹣b)2
(2)解:(m+n)2﹣4mn=(m﹣n)2
问题解决:
(x﹣y)2=(x+y)2﹣4xy
∵x+y=6,xy=3.
∴(x﹣y)2=36﹣12=24
【解析】(1)第一种方法为:大正方形面积﹣4个小长方形面积,第二种表示方法为:阴影部分正方形的面积;(2)利用(a+b)2﹣4ab=(a﹣b)2可求解.

练习册系列答案
相关题目