题目内容
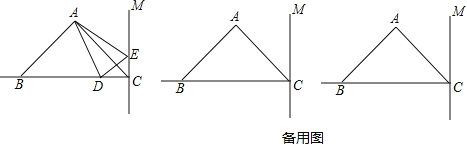
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=10cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒2厘米的速度运动,连接AD、AE,设运动时间为t秒.
(1)求AB的长;(2)当t为多少时,△ABD的面积为15cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(请在备用图中画出具体图形)
【答案】(1)5![]() ;(2)2或8; (3)2或10.
;(2)2或8; (3)2或10.
【解析】试题分析:(1)运用勾股定理直接求出;(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值;(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.
试题解析:(1)∵在△ABC中,AB=AC,∠BAC=90°,
∴2AB2=BC2,
∴AB=![]() =5
=5![]() cm;
cm;
(2)过A作AF⊥BC交BC于点F,
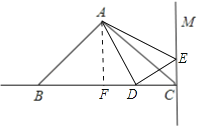
则AF=![]() BC=5cm,
BC=5cm,
∵S△ABD=15cm2,
∴AF×BD=30,
∴BD=6cm.
若D在B点右侧,则CD=4cm,t=2s;
若D在B点左侧,则CD=16cm,t=8s.
(3)动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动6秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=2t,BD=10﹣3t
∴2t=10﹣3t
∴t=2
证明:在△ABD和△ACE中,
∵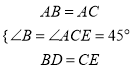 ,
,
∴△ABD≌△ACE(SAS).
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.
∵CE=2t,BD=3t﹣10,
∴2t=3t﹣10,
∴t=10
证明:在△ABD和△ACE中,
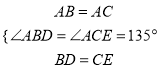
∴△ABD≌△ACE.

【题目】(2016浙江省温州市第22题)有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果 | 乙种糖果 | 丙种糖果 | |
单价(元/千克) | 15 | 25 | 30 |
千克数 | 40 | 40 | 20 |
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
