题目内容
23、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.当直线MN绕点C旋转到图1的位置时,易证:DE=AD+BE

(1)如果:当直线MN绕点C旋转到图2的位置时,那么试问线段DE,AD,BE又分别具有怎样的数量关系?请写出你的猜想.
(2)如果:当直线MN绕点C旋转到图3的位置时,那么试问线段DE,AD,BE又分别具有怎样的数量关系?请写出你的猜想.
(3)请你对上面(1)(2)中的一种情况给予证明.

(1)如果:当直线MN绕点C旋转到图2的位置时,那么试问线段DE,AD,BE又分别具有怎样的数量关系?请写出你的猜想.
DE=AD-BE
.(2)如果:当直线MN绕点C旋转到图3的位置时,那么试问线段DE,AD,BE又分别具有怎样的数量关系?请写出你的猜想.
DE=BE-AD
.(3)请你对上面(1)(2)中的一种情况给予证明.
分析:(1)、(2)要在图2、图3中寻找线段DE,AD,BE之间的数量关系,与图1一样,利用三角形全等就解决问题了.
(3)就其(1)问而言,只需要证明△ADC≌△CEB就可以了,利用AAS或ASA都可以证明.
(3)就其(1)问而言,只需要证明△ADC≌△CEB就可以了,利用AAS或ASA都可以证明.
解答:解:(1)DE=AD-BE;
(2)DE=BE-AD
(3)证明(1)
∵AD⊥MN,BE⊥MN
∴∠ADC=∠BEC=90°
∴∠2+∠3=90°
∵∠1+∠3=90°
∴∠1=∠2
∵AC=BC
∴△ADC≌△CEB
∴AD=CE,,CD=BE
∵DE=CE-CD
∴DE=AD-BE.

(2)DE=BE-AD
(3)证明(1)
∵AD⊥MN,BE⊥MN
∴∠ADC=∠BEC=90°
∴∠2+∠3=90°
∵∠1+∠3=90°
∴∠1=∠2
∵AC=BC
∴△ADC≌△CEB
∴AD=CE,,CD=BE
∵DE=CE-CD
∴DE=AD-BE.

点评:本题考查了图形的旋转,等腰直角三角形的性质,全等三角形的运用等多个知识点,在解决旋转问题的关键是变中求不变.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
在△ABC中,AC=8,BC=6,AB=10,则△ABC的外接圆半径长为( )
| A、10 | B、5 | C、6 | D、4 |
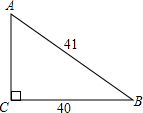 如图,在△ABC中,AC=
如图,在△ABC中,AC=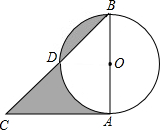 如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D.
如图所示,在△ABC中,AC与⊙O相切于点A,AC=AB=2,⊙O交BC于D. (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=