题目内容
 (2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=
(2013•松江区二模)如图,已知在△ABC中,AC=15,AB=25,sin∠CAB=| 4 | 5 |
(1)求BC的长;
(2)求△AED的面积.
分析:(1)过点作CF⊥AB于点F,由AC=15,sin∠CAB=
求出CF的长,由勾股定理求出AF的长,故可得出BF的长,在Rt△BCF中,根据勾股定理可求出BC的长;
(2)由(1)中CF⊥AB可知AD=2AF,根据BC的长可得出BE的长,过点E作EG⊥AB于点G,由相似三角形的判定定理可得出△BEG∽△BCF,故可得出EG的长,再根据S△AEG=
AD•EG即可得出结论.
| 4 |
| 5 |
(2)由(1)中CF⊥AB可知AD=2AF,根据BC的长可得出BE的长,过点E作EG⊥AB于点G,由相似三角形的判定定理可得出△BEG∽△BCF,故可得出EG的长,再根据S△AEG=
| 1 |
| 2 |
解答: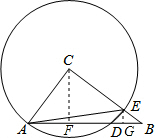 解:(1)过点作CF⊥AB于点F,
解:(1)过点作CF⊥AB于点F,
∵AC=15,sin∠CAB=
,
∴CF=AC•sin∠CAB=15×
=12,
在Rt△ACF中,
∵AC=15,CF=12,
∴AF=
=
=9,
∴BF=AB-AF=25-9=16,
在Rt△BCF中,
∵BF=16,CF=12,
∴BC=
=
=20;
(2)∵CF⊥AB,AF=9,
∴AD=2AF=18,
∵BC=20,CE=AC=15,
∴BE=BC-CE=20-15=5,
过点E作EG⊥AB于点G,
∵EG∥CF,
∴△BEG∽△BCF,
∴
=
,
=
,解得EG=3,
∴S△AEG=
AD•EG=
×18×3=27.
 解:(1)过点作CF⊥AB于点F,
解:(1)过点作CF⊥AB于点F,∵AC=15,sin∠CAB=
| 4 |
| 5 |
∴CF=AC•sin∠CAB=15×
| 4 |
| 5 |
在Rt△ACF中,
∵AC=15,CF=12,
∴AF=
| AC2-CF2 |
| 152-122 |
∴BF=AB-AF=25-9=16,
在Rt△BCF中,
∵BF=16,CF=12,
∴BC=
| BF2+CF2 |
| 162+122 |
(2)∵CF⊥AB,AF=9,
∴AD=2AF=18,
∵BC=20,CE=AC=15,
∴BE=BC-CE=20-15=5,
过点E作EG⊥AB于点G,
∵EG∥CF,
∴△BEG∽△BCF,
∴
| EG |
| CF |
| BE |
| BC |
| EG |
| 12 |
| 5 |
| 20 |
∴S△AEG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的是相似三角形的判定与性质,根据题意作出辅助线,构造出相似三角形是解答此题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 (2013•松江区二模)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,
(2013•松江区二模)如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,