题目内容
(2013•吴江市模拟)关于x的一元二次方程(k-2)x2-2(k-1)x+k+1=0有两个不同的实数根是xl和x2.
(1)求k的取值范围;
(2)当k=-2时,求4x12+6x2的值.
(1)求k的取值范围;
(2)当k=-2时,求4x12+6x2的值.
分析:(1)根据一元二次方程的定义和根的判别式的意义得到k-2≠0且△=4(k-1)2-4(k-2)(k+1)>0,然后解两个不等式得到它们的公共部分即可;
(2)先把k=-2代入原方程得到4x2-6x+1=0,根据根与系数的关系得xl+x2=
,xl•x2=
,由于xl是原方程的解,则4x12-6x1+1=0,即4x12=6x1-1,所以4x12+6x2=6x1-1+6x2=6(x1+x2)-1,然后利用整体思想计算即可.
(2)先把k=-2代入原方程得到4x2-6x+1=0,根据根与系数的关系得xl+x2=
| 3 |
| 2 |
| 1 |
| 4 |
解答:解:(1)根据题意得k-2≠0且△=4(k-1)2-4(k-2)(k+1)>0,
解得k<3且k≠0;
(2)当k=-2时,方程变形为4x2-6x+1=0,则xl+x2=
,xl•x2=
,
∵xl是原方程的解,
∴4x12-6x1+1=0,
∴4x12=6x1-1,
∴4x12+6x2=6x1-1+6x2=6(x1+x2)-1=6×
-1=8.
解得k<3且k≠0;
(2)当k=-2时,方程变形为4x2-6x+1=0,则xl+x2=
| 3 |
| 2 |
| 1 |
| 4 |
∵xl是原方程的解,
∴4x12-6x1+1=0,
∴4x12=6x1-1,
∴4x12+6x2=6x1-1+6x2=6(x1+x2)-1=6×
| 3 |
| 2 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义和根与系数的关系.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
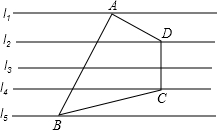 (2013•吴江市模拟)如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是( )
(2013•吴江市模拟)如图,已知直线l1∥l2∥l3∥l4∥l5,相邻两条平行直线间的距离相等且为1,如果四边形ABCD的四个顶点在平行直线上,∠BAD=90°且AB=3AD,DC⊥l4,则四边形ABCD的面积是( )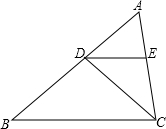 (2013•吴江市模拟)如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=4:5,AC=9.
(2013•吴江市模拟)如图,△ABC中,CD平分∠ACB交AB于D,DE∥BC交AC于E,若AD:DB=4:5,AC=9.