题目内容
【题目】如图,将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,连接AE,CF,AC.
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,①求菱形AECF的边长;②求折痕EF的长.
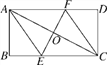
【答案】(1)证明见解析;(2)①5;②2![]() .
.
【解析】试题分析:(1)根据折叠的性质得OA=OC,EF⊥AC,EA=EC,再利用AD∥AC,得到∠FAC=∠ECA,则可根据“ASA”判断△AOF≌△COE,得到OF=OE,加上OA=OC,AC⊥EF,于是可根据菱形的判定方法得到四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BCCE=8x,AE=x,在Rt△ABE中,根据勾股定理得![]() 然后解方程即可得到菱形的边长;
然后解方程即可得到菱形的边长;
②先在Rt△ABC中,利用勾股定理计算出![]() 则
则![]() 然后在Rt△AOE中,利用勾股定理计算出
然后在Rt△AOE中,利用勾股定理计算出![]()
试题解析:证明:(1)∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,
在△AOF和△COE中,

∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BCCE=8x,AE=x,
在Rt△ABE中,∵![]()
∴![]() 解得x=5,
解得x=5,
即菱形的边长为5;
②在Rt△ABC中, ![]()
∴![]()
在Rt△AOE中,AE=5,
![]()
∴![]()

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目