��Ŀ����
����Ŀ���Ķ����ϣ�1���������ã�1���Ľ��۽�����⣨2�������⣨3����
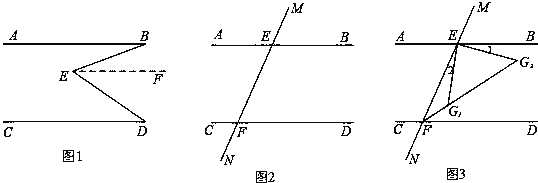
��1����ͼ1��AB��CD��EΪ����һ�㣬����BE��DE�õ���BED����֤����E����B+��D
�������������ģ�
����E��EF��AB������BEF����B��
��AB��CD����EF��CD��
���FED����D��
���BEF+��FED����B+��D��
����BED����B+��D��
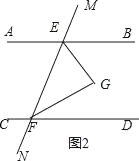
��2����ͼ2��������BEF�͡�EFD��ƽ���ߣ����߽��ڵ�G�������G�Ķ�������֤����IJ��룮
��3����ͼ3��EG1��EG2Ϊ��BEF�������1����2�������ߣ��ֱ����EFD��ƽ���߽��ڵ�G1��G2����֤����FG1E+��G2��180����
���𰸡���2����EGF��90������3���������.
��������
��2����ͼ2��ʾ�����룺��EGF=90�����ɽ��ۣ�1���á�EGF=��BEG+��GFD������EG��FG�ֱ�ƽ�֡�BEF�͡�EFD���õ���BEF=2��BEG����EFD=2��GFD������BE��CF����BEF+��EFD=180�������ǵõ�2��BEG+2��GFD=180�������ɵõ����ۣ�
��3����ͼ3������G1��G1H��AB�ɽ��ۣ�1���ɵá�G2=��1+��3����EG1F=��BEG1+��G1FD���õ���3=��G2FD������FG2ƽ�֡�EFD��á�4=��G2FD�����ڡ�1=��2�����ǵõ���G2=��2+��4�����ڡ�EG1F=��BEG1+��G1FD���õ���EG1F+��G2=��2+��4+��BEG1+��G1FD=��BEF+��EFD��Ȼ�����ƽ���ߵ����ʼ��ɵõ����ۣ�
֤������2����ͼ2��ʾ�����룺��EGF��90����
�ɽ��ۣ�1���á�EGF����BEG+��GFD��
��EG��FG�ֱ�ƽ�֡�BEF�͡�EFD��
���BEF��2��BEG����EFD��2��GFD��
��BE��CF��
���BEF+��EFD��180����
��2��BEG+2��GFD��180����
���BEG+��GFD��90����
�ߡ�EGF����BEG+��GFD��
���EGF��90����
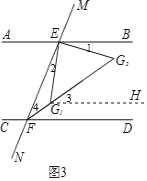
��3��֤������ͼ3������G1��G1H��AB��
��AB��CD����G1H��CD��
�ɽ��ۣ�1���ɵá�G2����1+��3����EG1F����BEG1+��G1FD��
���3����G2FD��
��FG2ƽ�֡�EFD��
���4����G2FD��
�ߡ�1����2��
���G2����2+��4��
�ߡ�EG1F����BEG1+��G1FD��
���EG1F+��G2����2+��4+��BEG1+��G1FD����BEF+��EFD��
��AB��CD��
���BEF+��EFD��180����
���EG1F+��G2��180����

 ��У����ϵ�д�
��У����ϵ�д�