题目内容
在图1至图4中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE和AD在同一直线上.
操作示例:
当AE<a时,如图1,在BA上选取适当的点G,BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置,恰能构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上,连接CH.由剪拼方法可得DH=BG,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图所示),
实践探究:
(1)小明判断出四边形FGCH是正方形,请你给出判断四边形FGCH是正方形的方法。
(2)经测量,小明发现图1中BG是AE一半,请你证明小明的发现是正确的。(提示:过点F作FM⊥AH,垂足为点M);
拓展延伸
类比图1的剪拼方法,请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图

操作示例:
当AE<a时,如图1,在BA上选取适当的点G,BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置,恰能构成四边形FGCH.
思考发现:小明在操作后发现:该剪拼方法是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上,连接CH.由剪拼方法可得DH=BG,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图所示),
实践探究:
(1)小明判断出四边形FGCH是正方形,请你给出判断四边形FGCH是正方形的方法。
(2)经测量,小明发现图1中BG是AE一半,请你证明小明的发现是正确的。(提示:过点F作FM⊥AH,垂足为点M);
拓展延伸
类比图1的剪拼方法,请你就图2至图4的三种情形分别画出剪拼成一个新正方形的示意图

(1)方法见解析;(2)证明见解析;(3)拼图见解析.
试题分析:(1)根据旋转的性质得出两三角形全等,求出三角形FGH是等腰直角三角形,并推出四个角是直角,根据正方形的判定推出即可;
(2)过点F作FM⊥AH,垂足为点M,求出ME=
 AE,证Rt△FMH≌Rt△HDC,推出MH=DC,即可得出答案;
AE,证Rt△FMH≌Rt△HDC,推出MH=DC,即可得出答案;拓展延伸:根据各个图形的特点,结合正方形的判定画出即可.
试题解析:(1)如图,连接GH,

∵△FEH是由△FAG绕点F逆时针旋转90°得到的,
∴△FGH是等腰直角三角形
∴FG=FH,∠FGH=∠FHG=45°,
同理:∠CGH=∠CHG=45°,
∴∠FGC=∠FHC=90°,
∴四边形FGCH是正方形;
(2)如图,过点F作FM⊥AH,垂足为点M,

∴∠FMH=90°
∵△FAE是等腰直角三角形,
∴ME=
 AE,
AE,∵∠FHM+∠HFM=90°,
∴∠FHM+∠CHD=90°
∴∠HFM=∠CHD,
∵四边形ABCD和四边形FGCH都是正方形,
∴FH=HC,∠FMH=∠CDH=90°,
在△FMH和△HDC中

∴Rt△FMH≌Rt△HDC,
∴MH=DC,
∵四边形ABCD是正方形,
∴CD=AB
∵ME=MH-EH,
∴BG=AB-AG,
∵△FEH是由△FAG绕点F逆时针旋转90°得到的,
∴AG=EH,
∴BG=ME=
 AE;
AE;拓展延伸:


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 MN.
MN.



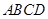 中,
中, 为
为 的中点,
的中点, 交
交 于点
于点 .
. ;
;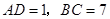 ,且
,且 平分
平分 时,求
时,求 的长.
的长.
 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;
90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;

