��Ŀ����
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
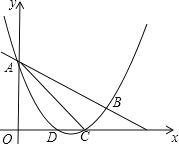
�������������ߵĽ���ʽ��tan��BAC��ֵ��
�������ڣ����������£�
��1��PΪy���Ҳ���������һ���㣬����PA������P��PQ��PA��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ���������������ACB���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��2����EΪ�߶�AC��һ�㣨�����˵㣩������DE��һ����M�ӵ�D���������߶�DE��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�EA��ÿ��![]() ����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�(ֱ��д���𰸣�
����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�(ֱ��д���𰸣�
���𰸡�������y=![]() x2-
x2-![]() x+3��tan��BAC
x+3��tan��BAC![]() ����������1����11��36������
����������1����11��36������![]() ��
��![]() ������
������![]() ��
��![]() ������2����E��������2��1����
������2����E��������2��1����
��������
���������������ֻ���A��C������������y=![]() x2+mx+n���Ϳɵõ������ߵĽ���ʽ��Ȼ�����ֱ��AB�������ߵĽ���B�����꣬����B��BH��x����H����ͼ1������BCH=��ACO=45����BC=
x2+mx+n���Ϳɵõ������ߵĽ���ʽ��Ȼ�����ֱ��AB�������ߵĽ���B�����꣬����B��BH��x����H����ͼ1������BCH=��ACO=45����BC=![]() ��AC=3
��AC=3![]() ���Ӷ��õ���ACB=90����Ȼ��������Ǻ����Ķ���Ϳ����tan��BAC��ֵ��
���Ӷ��õ���ACB=90����Ȼ��������Ǻ����Ķ���Ϳ����tan��BAC��ֵ��
��������1������P��PG��y����G������PGA=90�������P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG=x������APQ=��ACB=90��������G�ڵ�A���·���������PAQ=��CABʱ����PAQ�ס�CAB����ʱ��֤����PGA�ס�BCA���������������ε����ʿɵ�AG=3PG=3x������P��x��3-3x����Ȼ���P��x��3-3x�����������ߵĽ���ʽ���Ϳ������P������������PAQ=��CBAʱ����PAQ�ס�CBA��ͬ�����������P�����ꣻ����G�ڵ�A���Ϸ���ͬ�����������P�����ꣻ��2������E��EN��y����N����ͼ3����AE=![]() EN�����M�������˶������õ�ʱ��ɱ�ʾΪ
EN�����M�������˶������õ�ʱ��ɱ�ʾΪ![]() ������D����AC�ĶԳƵ�D��������D��E������D��E=DE��D��C=DC����D��CA=��DCA=45�����Ӷ��ɵ���D��CD=90����DE+EN=D��E+EN����������֮���߶���̿ɵã���D����E��N���㹲��ʱ��DE+EN=D��E+EN��С����ʱ��֤���ı���OCD��N�Ǿ��Σ��Ӷ���ND��=OC=3��ON=D��C=DC��Ȼ�������D�����꣬�Ӷ��õ�OD��ON��NE��ֵ�����ɵõ���E�����꣮
������D����AC�ĶԳƵ�D��������D��E������D��E=DE��D��C=DC����D��CA=��DCA=45�����Ӷ��ɵ���D��CD=90����DE+EN=D��E+EN����������֮���߶���̿ɵã���D����E��N���㹲��ʱ��DE+EN=D��E+EN��С����ʱ��֤���ı���OCD��N�Ǿ��Σ��Ӷ���ND��=OC=3��ON=D��C=DC��Ȼ�������D�����꣬�Ӷ��õ�OD��ON��NE��ֵ�����ɵõ���E�����꣮
�����������������A��0��3����C��3��0������y=![]() x2+mx+n����
x2+mx+n����
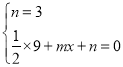 ����ã�
����ã� ��
��
�������ߵĽ���ʽΪy=![]() x2-
x2-![]() x+3��
x+3��
����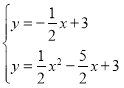 ����ã�
����ã�![]() ��
��![]() ��
��
����B��������4��1����
����B��BH��x����H����ͼ1��
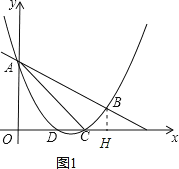
��C��3��0����B��4��1����
��BH=1��OC=3��OH=4��CH=4-3=1��
��BH=CH=1��
�ߡ�BHC=90����
���BCH=45����BC=![]() ��
��
ͬ������ACO=45����AC=3![]() ��
��
���ACB=180��-45��-45��=90����
��tan��BAC=![]() ��
��
��������1�����ڵ�P��ʹ����A��P��QΪ���������������ACB���ƣ�
����P��PG��y����G������PGA=90����
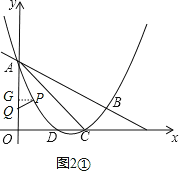
���P�ĺ�����Ϊx����P��y���Ҳ�ɵ�x��0����PG=x��
��PQ��PA����ACB=90����
���APQ=��ACB=90����
����G�ڵ�A���·���
����ͼ2��������PAQ=��CABʱ������PAQ�ס�CAB��
�ߡ�PGA=��ACB=90������PAQ=��CAB��
���PGA�ס�BCA��
��![]() ��
��
��AG=3PG=3x��
��P��x��3-3x����
��P��x��3-3x������y=![]() x2-
x2-![]() x+3����
x+3����
![]() x2-
x2-![]() x+3=3-3x��
x+3=3-3x��
�����ã�x2+x=0
��ã�x1=0����ȥ����x2=-1����ȥ����
����ͼ2��������PAQ=��CBAʱ������PAQ�ס�CBA��
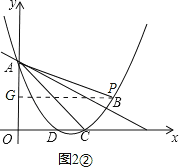
ͬ���ɵã�AG=![]() PG=
PG=![]() x����P��x��3-
x����P��x��3-![]() x����
x����
��P��x��3-![]() x������y=
x������y=![]() x2-
x2-![]() x+3����
x+3����
![]() x2-
x2-![]() x+3=3-
x+3=3-![]() x��
x��
�����ã�x2-![]() x=0
x=0
��ã�x1=0����ȥ����x2=![]() ��
��
��P��![]() ��
��![]() ����
����
����G�ڵ�A���Ϸ���
������PAQ=��CABʱ������PAQ�ס�CAB��
ͬ���ɵã���P������Ϊ��11��36����
������PAQ=��CBAʱ������PAQ�ס�CBA��
ͬ���ɵã���P������ΪP��![]() ��
��![]() ����
����
�������������������ĵ�P������Ϊ��11��36������![]() ��
��![]() ������
������![]() ��
��![]() ����
����
��2������E��EN��y����N����ͼ3��
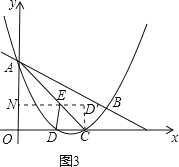
��Rt��ANE��EN=AEsin45��=![]() AE����AE=
AE����AE=![]() EN��
EN��
����M�������˶������õ�ʱ��Ϊ![]() ��
��
����D����AC�ĶԳƵ�D��������D��E��
����D��E=DE��D��C=DC����D��CA=��DCA=45����
���D��CD=90����DE+EN=D��E+EN��
��������֮���߶���̿ɵã�
��D����E��N���㹲��ʱ��DE+EN=D��E+EN��С��
��ʱ���ߡ�D��CD=��D��NO=��NOC=90����
���ı���OCD��N�Ǿ��Σ�
��ND��=OC=3��ON=D��C=DC��
����y=![]() x2-
x2-![]() x+3��
x+3��
��y=0ʱ����![]() x2-
x2-![]() x+3=0��
x+3=0��
��ã�x1=2��x2=3��
��D��2��0����OD=2��
��ON=DC=OC-OD=3-2=1��
��NE=AN=AO-ON=3-1=2��
����E��������2��1����