题目内容
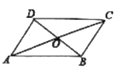
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A在y轴正半轴上,边AB、OA(AB>OA)的长分别是方程x2﹣11x+24=0的两个根,D是AB上的点,且满足![]() .
.
(1)矩形OABC的面积是 ,周长是 .
(2)求直线OD的解析式;
(3)点P是射线OD上的一个动点,当△PAD是等腰三角形时,求点P的坐标.

【答案】(1)S=24,C=22;(2)y=-x;(3)P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0);  ;
; 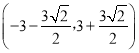
【解析】试题分析:(1)根据边AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,即可得到AO=3,AB=8,进而得出矩形OABC的面积以及矩形OABC的周长;
(2)根据![]() ,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
,AB=8,可得AD=3,再根据AO=3,进而得出D(-3,3),再根据待定系数法即可求得直线OD的解析式;
(3)根据△PAD是等腰三角形,分情况讨论,根据等腰直角三角形的性质,求得点P的坐标.
试题解析:(1)(1)∵x2-11x+24=0,
∴(x-3)(x-8)=0,
∴x1=3,x2=8,
∵AB、OA(AB>OA)的长分别是方程x2-11x+24=0的两个根,
∴AO=3,AB=8,
∴矩形OABC的面积=3×8=24,矩形OABC的周长=2×(3+8)=22,
故答案为:24,22;
(2)∵![]() ,AB=8,
,AB=8,
∴AD=3,
又∵AO=3,
∴D(-3,3),
设直线OD解析式为y=kx,则
3=-3k,即k=-1,
∴直线OD的解析式为y=-x;
(3)∵AD=AO=3,∠DAO=90°,
∴△AOD是等腰直角三角形,
∴∠ADO=45°,DO=3![]() ,
,
根据△PAD是等腰三角形,分4种情况讨论:
①如图所示,当AD=AP1=3时,点P1的坐标为(0,0);
②如图所示,当DA=DP2=3时,过P2作x轴的垂线,垂足为E,则
OP2=3![]() -3,△OEP2是等腰直角三角形,
-3,△OEP2是等腰直角三角形,
∴P2E=OE=![]() =3-
=3-![]() ,
,
∴点P2的坐标为(-3+![]() ,3-
,3-![]() );
);
③如图所示,当AP3=DP3时,∠DAP3=∠ADO=45°,
∴△ADP3是等腰直角三角形,
∴DP3=![]() =
=![]()
∴P3O=3![]() -
-![]() =
=![]() ,
,
过P3作x轴的垂线,垂足为F,则△OP3F是等腰直角三角形,
∴P3F=OF=![]() ,
,
∴点P3的坐标为(-![]() ,
, ![]() );
);
④如图所示,当DA=DP4=3时,P4O=3+3![]() ,
,
过P4作x轴的垂线,垂足为G,则△OP4G是等腰直角三角形,
∴P4G=OG=![]() +3,
+3,
∴点P4的坐标为(-3-![]() ,3+
,3+![]() );
);
综上所述,P点的坐标为(![]() ,
, ![]() );(0,0);
);(0,0); ![]() ;
; ![]()


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
第一次 | 第二次 | |
甲种货车的辆数 | 2辆 | 5辆 |
乙种货车的辆数 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?