题目内容
若方程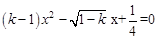 有两个实数根,则k的取值范围是(
)
有两个实数根,则k的取值范围是(
)
A.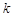 ≥1 B.
≥1 B.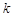 ≤1 C.
≤1 C.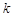 >1 D.
>1 D.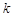 <1
<1
【答案】
D.
【解析】
试题分析:假设k=1,代入方程中检验,发现等式不成立,故k不能为1,可得出此方程为一元二次方程,进而有方程有解,得到根的判别式大于等于0,列出关于k的不等式,求出不等式的解集得到k的范围,且由负数没有平方根得到1-k大于0,得出k的范围,综上,得到满足题意的k的范围:
当k=1时,原方程不成立,故k≠1,
∴方程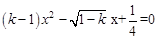 为一元二次方程,
为一元二次方程,
又此方程有两个实数根,
∴b2-4ac=(-1−k)2-4×(k-1)×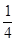 =1-k-(k-1)=2-2k≥0,
=1-k-(k-1)=2-2k≥0,
解得:k≤1,1-k>0,
综上k的取值范围是k<1.
故选D.
考点:根的判别式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目