题目内容
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.
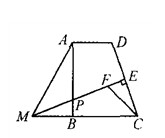
(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°-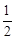 ∠FCM.
∠FCM.
(1) 连结MD,
 E是DC的中点,且ME⊥DC
E是DC的中点,且ME⊥DC
 EM是CD的垂直平分线
EM是CD的垂直平分线
 MD=MC
MD=MC
△AMD和△FMC中
AM=FM
MD=MC
AD=FC
 △AMD
△AMD △FMC (SSS)
△FMC (SSS)

 MAD=
MAD= MFC=125
MFC=125
又 AD∥BC 且∠ABC=90
AD∥BC 且∠ABC=90

 BAD=90
BAD=90

 MAB=35
MAB=35
 MB=
MB= AM
AM
即MB= MF
MF
 MF=2MB
MF=2MB
(2)  MD=MC
且ME⊥DC
MD=MC
且ME⊥DC
 ME平分
ME平分 DMC
DMC

 FMC=
FMC=
 DMC
DMC
又  AD∥MC
AD∥MC

 DMC=
DMC= ADM
ADM
又 △AMD
△AMD △FMC
△FMC

 ADM=
ADM= FCM
FCM

 DMC=
DMC= FCM
FCM

 FMC=
FMC=
 FCM
FCM
Rt△BPM中
 MPB=90-
MPB=90- FMC
FMC
=90-
 FCM
FCM
【解析】(1)连接MD,由于点E是DC的中点,ME⊥DC,所以MD=MC,然后利用已知条件证明△AMD≌△FMC,根据全等三角形的性质可以推出∴∠MAD=∠MFC=120°,接着得到∠MAB=30°,再根据30°的角所对的直角边等于斜边的一半即可证明AM=2BM;
(2)利用(1)的结论得到∠ADM=∠FCM,又AD∥BC,所以∠ADM=∠CMD,由此得到∠CMD=∠FCM,再利用等腰三角形的性质即可得到∠CME= ∠FCM,再根据已知条件即可解决问题.
∠FCM,再根据已知条件即可解决问题.

 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.