题目内容
如图，OA、OB是⊙O的半径，∠O=40°，∠B=50°，则∠A等于
- A.80°
- B.70°
- C.60°
- D.30°
D
分析：先根据圆周角定理求出∠C的度数，由三角形内角和定理可得出∠BDC的度数，由对顶角相等可知∠ADO的度数，再在△AOD中由三角形内角和定理即可求出∠AA的度数．
解答：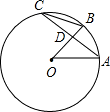
解：∵∠O=40°，
∴∠C=
∠O=20°，
∴∠BDC=180°-∠B-∠C=180°-50°-20°=110°，
∴∠ADO=∠BDC=110°，
∴∠A=180°-∠ADO-∠O=180°-110°-40°=30°．
故选D．
点评：本题考查的是圆周角定理及三角形内角和定理，熟知“在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半”是解答此题的关键．
分析：先根据圆周角定理求出∠C的度数，由三角形内角和定理可得出∠BDC的度数，由对顶角相等可知∠ADO的度数，再在△AOD中由三角形内角和定理即可求出∠AA的度数．
解答：
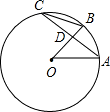解：∵∠O=40°，∴∠C=
∠O=20°，∴∠BDC=180°-∠B-∠C=180°-50°-20°=110°，
∴∠ADO=∠BDC=110°，
∴∠A=180°-∠ADO-∠O=180°-110°-40°=30°．
故选D．
点评：本题考查的是圆周角定理及三角形内角和定理，熟知“在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半”是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
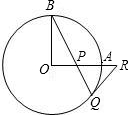如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的直线交OA延长线于点R，且RP=RQ
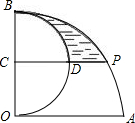如图，OA、OB是两条互相垂直的半径，且OA=4，C为OB的中点，以OB为直径作半圆，CP∥OA，交
16、如图，OA和OB是⊙O的半径，并且OA⊥OB．P是OA上的任意一点，BP的延长线交⊙O于点Q，点R在OA的延长线上，且RP=RQ．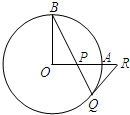
如图，OA和OB是⊙O的半径，OB=2，OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的⊙O的切线交OA延长线于点R．
如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的直线交OA延长线于点R，且RP=RQ