题目内容
16、如图，OA和OB是⊙O的半径，并且OA⊥OB．P是OA上的任意一点，BP的延长线交⊙O于点Q，点R在OA的延长线上，且RP=RQ．（1）求证：RQ是⊙O的切线；
（2）求证：OB2=PB•PQ+OP2；
（3）当RA≤OA时，试确定∠B的取值范围．
分析：（1）要证明RQ是⊙O的切线只要证明∠OQR=90°即可；
（2）先证明△BCP∽△AQP，从而得到PB•PQ=PC•PA，整理即可得到OB2=PB•PQ+OP2；
（3）分别考虑当RA=OA时或与A重合时，∠B的度数，从而确定其取值范围．
（2）先证明△BCP∽△AQP，从而得到PB•PQ=PC•PA，整理即可得到OB2=PB•PQ+OP2；
（3）分别考虑当RA=OA时或与A重合时，∠B的度数，从而确定其取值范围．
解答：
证明：（1）连接OQ；
∵OB=OC，PR=RQ；
∴∠OBP=∠OQP，∠RPQ=∠RQP；
∵∠OBP+∠BPO=90°，∠BPO=∠RPQ；
∴∠OQP+∠RQP=90°；
即∠OQR=90°，
∴RQ是⊙O的切线．
证明：（2）延长AO⊙O交于点C；
∵∠BPC=∠QPA，∠BCP=∠AQP，
∴△BCP∽△AQP，
∴PB•PQ=PC•PA=（OC+OP）（OA-OP）=（OB+OP）（OB-OP）=OB2-OP2，
∴OB2=PB•PQ+OP2．
解：（3）当RA=OA时，∠R=30°，易得∠B=15°，当R与A重合时，∠B=45°；
∵R是OA延长线上的点，
∴R与A不重合，
∴∠B≠45°；
又∵RA≤OA，
∴∠B＜45°，
∴15°≤B＜45°．
证明：（1）连接OQ；∵OB=OC，PR=RQ；
∴∠OBP=∠OQP，∠RPQ=∠RQP；
∵∠OBP+∠BPO=90°，∠BPO=∠RPQ；
∴∠OQP+∠RQP=90°；
即∠OQR=90°，
∴RQ是⊙O的切线．
证明：（2）延长AO⊙O交于点C；
∵∠BPC=∠QPA，∠BCP=∠AQP，
∴△BCP∽△AQP，
∴PB•PQ=PC•PA=（OC+OP）（OA-OP）=（OB+OP）（OB-OP）=OB2-OP2，
∴OB2=PB•PQ+OP2．
解：（3）当RA=OA时，∠R=30°，易得∠B=15°，当R与A重合时，∠B=45°；
∵R是OA延长线上的点，
∴R与A不重合，
∴∠B≠45°；
又∵RA≤OA，
∴∠B＜45°，
∴15°≤B＜45°．
点评：此题考查了学生对切线的判定及相似三角形的判定等知识点的综合运用．
练习册系列答案
相关题目
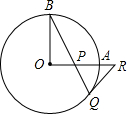如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的⊙O的切线交OA延长线于点R．
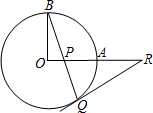如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于Q，过Q的⊙O的切线交OA的延长线于R．求证：RP=RQ．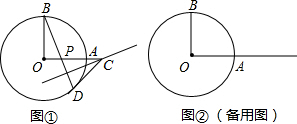
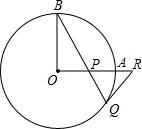如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于点Q，过点Q的直线交OA延长线于点R，且RP=RQ