题目内容
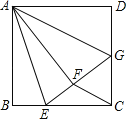
【题目】 如图,正方形ABCD的对角线AC、BD交于点O,∠ABD的平分线BE交AC于G,交AD于F,且DE⊥BE.
(1)求证:DE=![]() BF;
BF;
(2)若BG=![]() ,求BF的长.
,求BF的长.
【答案】(1)见解析;(2)BF=2
【解析】
(1)延长DE和BA交于M,根据ASA证△MBE≌△DBE,推出DE=![]() DM,根据ASA证△ABF≌△ADM,推出BF=DM即可;
DM,根据ASA证△ABF≌△ADM,推出BF=DM即可;
(2)关键正方形性质推出∠ADB=∠ABD,证△ABG和△DBF相似,得出比例式,代入求出即可.
(1)证明:延长DE和BA交于M,
∵DE⊥BE,
∴∠BED=∠BEM=90°,
∵BF平分∠ABD,
∴∠ABE=∠DBE,
在△MBE和△DBE中
∠MEB=∠DEB,BE=BE,∠MBE=∠DBE,
∴△MBE≌△DBE,
∴DE=EM=![]() DM,
DM,
∵正方形ABCD,
∴AB=AD,∠MAD=∠BAD=90°,
∵∠EFD=∠AFB,
∴∠MDA=∠ABF,
在△ABF和△ADM中
∠MAD=∠BAF,AB=AD,∠ADM=∠ABF,
∴△ABF≌△ADM,
∴BF=DM,
∴DE=![]() BF.
BF.
(2)解:∵正方形ABCD,
∴∠BAC=∠ADB=![]() ×90°=45°,
×90°=45°,
∵∠ABG=∠DBG,
∴△ABG∽△DBF,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴BF=2.

【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.

【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
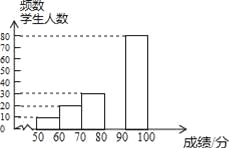
请根据所给信息,解答下列问题:
(1)a=______,b=______;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在_____________分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?
【题目】水是人类的生命之源,为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策,下表是昆明市居民“一表一户”生活用水阶梯式计费价格表的部分信息,请解答:
自来水销售价格 | |
每户每月用水量 | 单位:元/吨 |
15吨及以下 | a |
超过15吨但不超过25吨的部分 | b |
超过25吨的部分 | 5 |
(1)小王家今年3月份用水22吨,要交水费 元(用含a,b的代数式表示);
(2)小王家今年4月份用水21吨,交水费48元;邻居小李家4月份用水27吨,交水费70元,求a,b的值;
(3)如果小王家5月份用水水费计划不超过67元,则小王家5月份最多可用水多少吨?