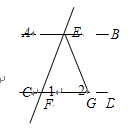题目内容
如图，如果AB∥CD，AE平分∠BAC，CE平分∠ACD，试说明AE⊥CE。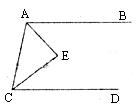
证明见解析
AE⊥CE
∵AB∥CD
∴∠BAC+∠ACD=180°. [
∵AE平分∠BAC,CE平分∠ACD
∴∠EAC+∠ACE=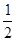
×180°=90°
∴∠AEC=90°
∴AE⊥CE
根据平行线的性质求得∠BAC+∠ACD=180°，利用角平分线求得∠EAC+∠ACE=90°，从而求得结论
∵AB∥CD
∴∠BAC+∠ACD=180°. [
∵AE平分∠BAC,CE平分∠ACD
∴∠EAC+∠ACE=
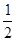×180°=90°∴∠AEC=90°
∴AE⊥CE
根据平行线的性质求得∠BAC+∠ACD=180°，利用角平分线求得∠EAC+∠ACE=90°，从而求得结论
练习册系列答案
相关题目
