题目内容
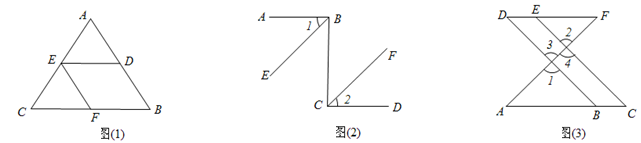
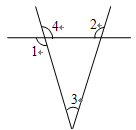
直线AB、CD相交于点O,OE是∠AOD的平分线,∠FOC="100" º,∠1="35" º。求∠2与∠3的度数。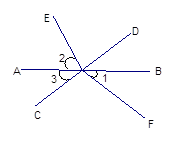

∵∠FOC=100°,∠1=35°,AB为直线,
∴∠3+∠FOC+∠1=180°,
∴∠3=180°-100°-35°=45°.
∠3与∠AOD互补,
∴∠AOD=180°-∠3=135°,
∵OE平分∠AOD,
∴∠2=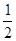 ∠AOD=67.5°.
∠AOD=67.5°.
故可得∠2=67.5°,∠3=45°.
∴∠3+∠FOC+∠1=180°,
∴∠3=180°-100°-35°=45°.
∠3与∠AOD互补,
∴∠AOD=180°-∠3=135°,
∵OE平分∠AOD,
∴∠2=
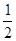 ∠AOD=67.5°.
∠AOD=67.5°.故可得∠2=67.5°,∠3=45°.
由已知∠FOC=100°,∠1=35°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为邻补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.

练习册系列答案
相关题目

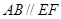 ,(已知)
,(已知)
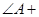 =
=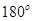 .( )
.( )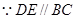 ,(已知)
,(已知)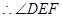 = ,( )
= ,( ) = ;( )
= ;( )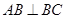 ,
,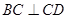 ,
,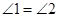 .试判断
.试判断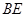 与
与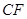 的关系,并说明你的理由.
的关系,并说明你的理由.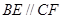 ,理由是:
,理由是: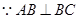 ,
,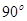 .( )
.( )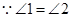 ,( )
,( )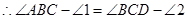 ,即
,即 .
.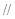 ;(
;(  点为
点为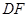 上的点,
上的点,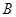 点为
点为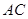 上的点,
上的点, ,试说明:
,试说明: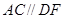 .
.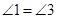 ,( )
,( )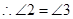 ,(等量代换)
,(等量代换) ,( )
,( )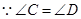 ,(已知)
,(已知) ,( )
,( )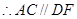 .( )
.( )
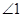 与
与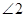 是内错角
是内错角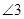 是同位角
是同位角 是同旁内角
是同旁内角