ΧβΡΩΡΎ»ί
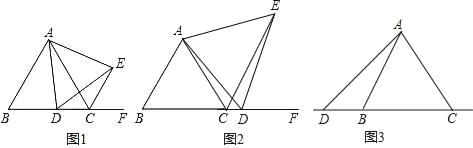
ΓΨΧβΡΩΓΩ“―÷ΣΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψDΈΣ÷±œΏBC…œΒΡ“ΜΕ·Βψ(ΒψD≤Μ”κBΓΔC÷ΊΚœ)Θ§“‘ADΈΣ±ΏΉςΒ»±ΏΓςADE(ΕΞΒψAΓΔDΓΔEΑ¥Ρφ ±’κΖΫœρ≈≈Ν–)Θ§Ν§Ϋ”CEΘ°
(1)»γΆΦ1Θ§Β±ΒψD‘Ύ±ΏBC…œ ±Θ§«σ÷ΛΘΚΔΌBDΘΫCEΘ§ΔΎACΘΫCE+CDΘΜ
(2)»γΆΦ2Θ§Β±ΒψD‘Ύ±ΏBCΒΡ―”≥ΛœΏ…œ«“ΤδΥϊΧθΦΰ≤Μ±δ ±Θ§Ϋα¬έACΘΫCE+CD «Ζώ≥…ΝΔΘΩ»τ≤Μ≥…ΝΔΘ§«κ–¥≥ωACΓΔCEΓΔCD÷°Φδ¥φ‘ΎΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
(3)»γΆΦ3Θ§Β±ΒψD‘Ύ±ΏBCΒΡΖ¥œρ―”≥ΛœΏ…œ«“ΤδΥϊΧθΦΰ≤Μ±δ ±Θ§≤Ι»ΪΆΦ–ΈΘ§≤Δ÷±Ϋ”–¥≥ωACΓΔCEΓΔCD÷°Φδ¥φ‘ΎΒΡ ΐΝΩΙΊœΒΘ°
ΓΨ¥πΑΗΓΩ(1)ΔΌ÷ΛΟςΦϊΫβΈωΘΜΔΎ÷ΛΟςΦϊΫβΈωΘΜ(2)ACΘΫCE+CD≤Μ≥…ΝΔΘ§ACΓΔCEΓΔCD÷°Φδ¥φ‘ΎΒΡ ΐΝΩΙΊœΒ «ΘΚACΘΫCE©¹CDΘ§άμ”…ΦϊΫβΈωΘΜ(3)≤ΙΆΦΦϊΫβΈωΘΜACΘΫCD©¹CEΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΦΑΒ» ΫΒΡ–‘÷ ÷ΛΟςΓςABDΓ’ΓςACEΘ§¥”ΕχΒΟ≥ωΫα¬έΘΜ
Θ®2Θ©ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΦΑΒ» ΫΒΡ–‘÷ ΨΆΩ…“‘ΒΟ≥ωΓςABDΓ’ΓςACEΘ§ΨΆΩ…“‘ΒΟ≥ωBDΘΫCEΘ§ΨΆΩ…“‘ΒΟ≥ωACΘΫCE©¹CDΘΜ
Θ®3Θ©œ»ΗυΨίΧθΦΰΜ≠≥ωΆΦ–ΈΘ§ΗυΨίΒ»±Ώ»ΐΫ«–ΈΒΡ–‘÷ ΦΑΒ» ΫΒΡ–‘÷ ΨΆΩ…“‘ΒΟ≥ωΓςABDΓ’ΓςACEΘ§ΨΆΩ…“‘ΒΟ≥ωBDΘΫCEΘ§ΨΆΩ…“‘ΒΟ≥ωACΘΫCD©¹CEΘ°
(1)ΓΏΓςABCΚΆΓςADEΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫACΘΫBCΘ§ADΘΫAEΘ§ΓœBACΘΫΓœDAEΘΫ60ΓψΘ°
ΓύΓœBAC©¹ΓœCADΘΫΓœDAE©¹ΓœCADΘ§Φ¥ΓœBADΘΫΓœCAEΘ°
‘ΎΓςABDΚΆΓςACE÷–Θ§
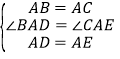 Θ§
Θ§
ΓύΓςABDΓ’ΓςACE(SAS)Θ§
ΓύBDΘΫCEΘ°
ΓΏBCΘΫBD+CDΘ§ACΘΫBCΘ§
ΓύACΘΫCE+CDΘΜ
(2)ACΘΫCE+CD≤Μ≥…ΝΔΘ§
ACΓΔCEΓΔCD÷°Φδ¥φ‘ΎΒΡ ΐΝΩΙΊœΒ «ΘΚACΘΫCE©¹CDΘ°
άμ”…ΘΚΓΏΓςABCΚΆΓςADEΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫACΘΫBCΘ§ADΘΫAEΘ§ΓœBACΘΫΓœDAEΘΫ60ΓψΘ°
ΓύΓœBAC+ΓœCADΘΫΓœDAE+ΓœCADΘ§
ΓύΓœBADΘΫΓœCAE
‘ΎΓςABDΚΆΓςACE÷–Θ§
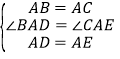
ΓύΓςABDΓ’ΓςACE(SAS)
ΓύBDΘΫCE
ΓύCE©¹CDΘΫBD©¹CDΘΫBCΘΫACΘ§
ΓύACΘΫCE©¹CDΘΜ
(3)≤Ι»ΪΆΦ–Έ(»γΆΦ)
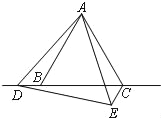
ACΓΔCEΓΔCD÷°Φδ¥φ‘ΎΒΡ ΐΝΩΙΊœΒ «ΘΚACΘΫCD©¹CEΘ°
άμ”…ΘΚΓΏΓςABCΚΆΓςADEΕΦ «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫACΘΫBCΘ§ADΘΫAEΘ§ΓœBACΘΫΓœDAEΘΫ60ΓψΘ°
ΓύΓœBAC©¹ΓœBAEΘΫΓœDAE©¹ΓœBAEΘ§
ΓύΓœBADΘΫΓœCAE
‘ΎΓςABDΚΆΓςACE÷–Θ§
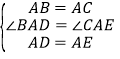
ΓύΓςABDΓ’ΓςACE(SAS)
ΓύBDΘΫCEΘ°
ΓΏBCΘΫCD©¹BDΘ§
ΓύBCΘΫCD©¹CEΘ§
ΓύACΘΫCD©¹CEΘ°

 ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ
ΟœΫ®ΤΫΟϊ–ΘΩΦΨμœΒΝ–¥πΑΗ