题目内容
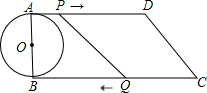 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13厘米,BC=16厘米,CD=5厘米,AB为⊙O的直径,动点P沿AD方向从点A开始向点D以1厘米/秒的速度运动,动点Q沿CB方向从点C开始向点B以2厘米/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=13厘米,BC=16厘米,CD=5厘米,AB为⊙O的直径,动点P沿AD方向从点A开始向点D以1厘米/秒的速度运动,动点Q沿CB方向从点C开始向点B以2厘米/秒的速度运动,点P、Q分别从A、C两点同时出发,当其中一点停止时,另一点也随之停止运动.(1)求⊙O的直径;
(2)求四边形PQCD的面积y关于P、Q运动时间t的函数关系式,并求当四边形PQCD为等腰梯形时,四边形PQCD的面积;
(3)是否存在某一时刻t,使直线PQ与⊙O相切?若存在,求出t的值;若不存在,请说明理由.
分析:(1)过点D作DE⊥BC于E,则四边形ABED是矩形,AB=ED,所以求出DE,就求出了圆的直径.
(2)要求四边形PQCD的面积,只需用t表达出CQ和PD.当四边形PQCD为等腰梯形时,CQ-PD=2CE,即2t-(13-t)=6,即可求出t的值,从而确定四边形的面积.
(3)先假设存在,构造直角三角形,利用勾股定理得出方程,解方程,若方程有解,则存在,若方程无解,则不存在.
(2)要求四边形PQCD的面积,只需用t表达出CQ和PD.当四边形PQCD为等腰梯形时,CQ-PD=2CE,即2t-(13-t)=6,即可求出t的值,从而确定四边形的面积.
(3)先假设存在,构造直角三角形,利用勾股定理得出方程,解方程,若方程有解,则存在,若方程无解,则不存在.
解答:解:(1)过点D作DE⊥BC于E,
BE=AD=13,
∵BC=16,
∴EC=3,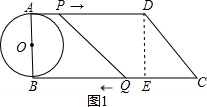
在Rt△DCE中,由于DC=5,
则DE=
=4,
所以圆的直径为4厘米;
(2)当P,Q运动t秒时,由点P,Q的运动速度为1厘米/秒和2厘米/秒,
所以PD=(13-t)厘米,CQ=2t厘米,
所以四边形PQCD的面积为y=
AB•(PD+CQ),
即y=2t+26(0<t≤8);
当四边形PQCD为等腰梯形时,CQ-PD=2CE,
所以2t-(13-t)=6,解得t=
,
这时y四边形PQCD=
厘米2.
(3)存在.若PQ与圆相切,切点G,作PH⊥BC于H,
 所以PA=PG=t,QG=QB=16-2t,
所以PA=PG=t,QG=QB=16-2t,
又得到QH=QB-HB=(16-2t)-t=16-3t,PQ=BQ+AP=16-t,
根据勾股定理得PQ2=PH2+QH2,
所以(16-t)2=16+(16-3t)2,
解得t1=4+
,t2=4-
,
因为4+
和4-
都在0<t≤8内,所以在t=(4+
)秒或t=(4-
)秒时,直线PQ与圆相切.
BE=AD=13,
∵BC=16,
∴EC=3,

在Rt△DCE中,由于DC=5,
则DE=
| 52-32 |
所以圆的直径为4厘米;
(2)当P,Q运动t秒时,由点P,Q的运动速度为1厘米/秒和2厘米/秒,
所以PD=(13-t)厘米,CQ=2t厘米,
所以四边形PQCD的面积为y=
| 1 |
| 2 |
即y=2t+26(0<t≤8);
当四边形PQCD为等腰梯形时,CQ-PD=2CE,
所以2t-(13-t)=6,解得t=
| 19 |
| 3 |
这时y四边形PQCD=
| 116 |
| 3 |
(3)存在.若PQ与圆相切,切点G,作PH⊥BC于H,
 所以PA=PG=t,QG=QB=16-2t,
所以PA=PG=t,QG=QB=16-2t,又得到QH=QB-HB=(16-2t)-t=16-3t,PQ=BQ+AP=16-t,
根据勾股定理得PQ2=PH2+QH2,
所以(16-t)2=16+(16-3t)2,
解得t1=4+
| 14 |
| 14 |
因为4+
| 14 |
| 14 |
| 14 |
| 14 |
点评:本题是一个动点问题,解题时要善于将动点问题转化为静态题.此题是一个大综合题,难度较大,有利于培养同学们的钻研精神和坚韧不拔的意志品质.

练习册系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.