题目内容
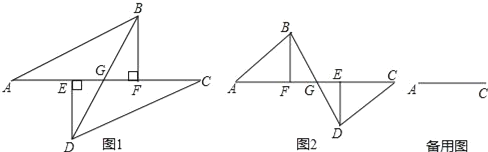
【题目】如图1所示，点E、F在线段AC上，过E，F分别作DE⊥AC，BF⊥AC，垂足分别为点E，F；DE，BF分别在线段AC的两侧，且AE=CF，AB=CD，BD与AC相交于点G.
(1)求证：EG=GF；
(2)若点E在F的右边，如图2时，其余条件不变，上述结论是否成立？请说明理由.
(3)若点E、F分别在线段CA的延长线与反向延长线上，其余条件不变，(1)中结论是否成立？(要求：在备用图中画出图形，直接判断，不必说明理由)
【答案】(1)证明见解析；(2)成立，理由见解析；(3)成立，图形见解析.
【解析】
(1)先利用HL证明Rt△ABF≌Rt△CDE，从而得到ED=FB，然后再根据AAS证明△BFG≌△DGE，从而可证得EG=FG；
(2)先证AF=EC，然后利用HL证明Rt△ABF≌Rt△CDE，从而得到BF=DE，然后利用AAS证明△BFG≌△DGE，从而可得到EG=FG；
(3)先根据要求画出图形，然后依据HL证明Rt△ABF≌Rt△CDE，从而得到BF=DE，然后利用AAS证明△BFG≌△DGE，从而可得到EG=FG.
解：(1)证明：∵DE⊥AC，BF⊥AC，
∴∠DEG=∠BFG=90°.
∵AE=CF，
∴AE+EF=CF+EF.
∴AF=CE.
在Rt△ABF和Rt△CDE中，
∴Rt△ABF≌Rt△CDE(HL)，
∴BF=DE.
在△BFG和△DEG中
，
∴△BFG≌△DGE(AAS).
∴EG=FG.
(2)解：(1)中结论依然成立.
理由如下：∵AE=CF，
∴AE﹣EF=CF﹣EF.
∴AF=CE.
∵DE⊥AC，BF⊥AC，
∴∠DEG=∠BFG=90°.
在Rt△ABF和Rt△CDE中，
∴Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
在△BFG和△DEG中，
∴△BFG≌△DGE(AAS).
∴EG=FG.
(3)(1)中结论依然成立.
如图所示：
理由如下：∵AE=CF，
∴AE+AC=CF+AC.
∴CE=AF.
∵DE⊥AC，BF⊥AC，
∴∠DEG=∠BFA=90°.
在Rt△ABF和Rt△CDE中，
∴Rt△ABF≌Rt△CDE(HL).
∴BF=DE.
在△BFG和△DEG中，
∴△BFG≌△DGE(AAS).
∴EG=FG.
