题目内容
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+( )2=﹣
x+( )2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
【答案】有错误,在第四步,错误的原因是在开方时对b2﹣4ac的值是否是非负数没有进行讨论.正确步骤见解析.
【解析】
①检查原题中的解题过程是否有误:在第四步时,在开方时对b2-4ac的值是否是非负数没有进行讨论;②更正:分类讨论b2-4ac≥0和b2-4ac<0时,原方程的根是什么.
解:有错误,在第四步.
错误的原因是在开方时对b2﹣4ac的值是否是非负数没有进行讨论.
正确步骤为:(x+![]() )2=
)2=![]() ,
,
①当b2﹣4ac≥0时,
x+![]() =±
=±![]() ,
,
x+![]() =±
=±![]() ,
,
x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() .
.
②当b2﹣4ac<0时,原方程无解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
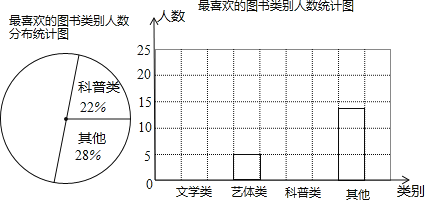
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.