��Ŀ����
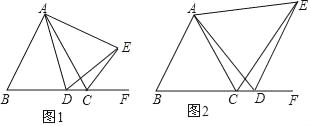
����Ŀ����ͼ1��ͼ3�У���B���߶�AC���е㣬��D���߶�CE���е㣮�ı���BCGF���ı���CDHN���������Σ�AE���е���M��
(1)��ͼ1����E��AC���ӳ����ϣ���N���G�غ�ʱ����M���C�غϣ���֤��FM=MH��FM��MH��
(2)��ͼ1�е�CE�Ƶ�C˳ʱ����תһ����ǣ��õ�ͼ2����֤����FMH�ǵ���ֱ�������Σ�
(3)��ͼ2�е�CE���̵�ͼ3���������FMH���ǵ���ֱ����������(����˵������)

���𰸡�(1)֤����������(2)֤����������(3)��FMH���ǵ���ֱ�������Σ�
��������
(1)���������ε����ʿɵ�FB=BM=MD=DH��Ȼ���������߽DZ���֤����FBM����MDHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�FM=MH���������FMH=90�����õ�FM��HM��Ȼ����ݵ���ֱ�������εĶ���֤�����ɣ�(2)����MB��MD����FM��AC���ڵ�P�����������ε���λ��ƽ���ڵ����߲��ҵ��ڵ����ߵ�һ��ɵ�MD��BC����MD=BC=BF��MB��CD����MB=CD=DH��Ȼ��õ��ı���BCDM��ƽ���ı��β������CBM=��CDM���������FBM=��MDH��Ȼ���������߽DZ���֤����FBM����MDHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�FM=MH��ȫ�������ζ�Ӧ����ȿɵá�MFB=��HMD��������ֱ��ƽ�У��ڴ�����ȿɵá�APM=��FMD��Ȼ����������ε�һ����ǵ������������ڵ������ڽǵĺ������FMH=��FBP=90�����ٸ��ݵ���ֱ�������εĶ���֤�����ɣ�(3)֤������ͬ(2)��
(1)֤�������ı���BCGFΪ�����Σ�
��BF=BM=MN����FBM=90����
���ı���CDHNΪ�����Σ�
��DM=DH=MN����HDM=90����
��BF=BM=MN��DM=DH=MN��
��BF=BM=DM=DH��
��BF=DH����FBM=��HDM��BM=DM��
���FBM�ա�HDM��
��FM=MH��
�ߡ�FMB=��DMH= 45����
���FMH=90����
��FM��HM��
(2)֤��������MB��MD����ͼ2����FM��AC���ڵ�P��
��B��D��M�ֱ���AC��CE��AE���е㣬
��MD��BC����MD=![]() AC=BC=BF��MB��CD����MB=
AC=BC=BF��MB��CD����MB=![]() CE=CD=DH��
CE=CD=DH��
���ı���BCDM��ƽ���ı��Σ�
���CBM=��CDM��
�ߡ�FBP=��HDC��
���FBM=��MDH��
��MD =BF����FBM=��MDH��MB=DH��
���FBM�ա�MDH��SAS����
��FM=MH���ҡ�MFB=��HMD��
��BC��MD��
���APM=��FMD��
���FMH=��FMD-��HMD=��APM-��MFB=��FBP=90����
���FMH�ǵ���ֱ�������Σ�

(3)��FMH���ǵ���ֱ�������Σ�
����MB��MD����ͼ3����FM��AC���ڵ�P��
��B��D��M�ֱ���AC��CE��AE���е㣬
��MD��BC����MD=BC=BF��MB��CD����MB=CD=DH��
���ı���BCDM��ƽ���ı��Σ�
���CBM=��CDM��
�֡ߡ�FBP=��HDC��
���FBM=��MDH��
����FBM����MDH��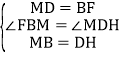 ��
��
���FBM�ա�MDH��SAS����
��FM=MH���ҡ�MFB=��HMD��
��BC��MD��
���APM=��FMD��
���FMH=��FMD-��HMD=��APM-��MFB=��FBP=90����
���FMH�ǵ���ֱ�������Σ�

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�