题目内容
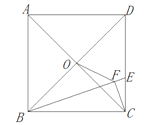
【题目】如图，在平行四边形ABCD中，∠BCD和∠ABC的平分线分别交AD于E，G两点，CE，BG相交于点O
(1)求证：AG=DE.
(2)已知AB=4，AD=5，
①求
的值.
②求四边形ABOE的面积与△BOC的面积之比.
【答案】(1)证明见解析；(2)①
=
；②S四ABOE：S△OBC=23：25.
【解析】
（1）由平行四边形的性质和角平分线得出∠ABG=∠AGB，得出AG=AB，同理可证DE=DC，推出AG=DE即可解决问题．
（2）①求出EG的值，利用平行线的性质即可解决问题．
②连接OA．设△AEP的面积为S．求出四边形ABOE，△OBC的面积即可解决问题．
解：(1)∵BG平分∠ABC，CE平分∠BCD
∴∠ABG=∠CBG,∠BCE∠DCE
∵AD∥BC
∴∠CBG=∠AGB,∠BCE=∠CED
∴AB=AG,CD=DE
∵AB=CD
∴AG=DE；
(2)①∵AB=4，AD=5
∴AG=DG=4，AE=AD -DE=1，GD=AD -AG=1
∴EG=AD-AE-DG=3
∵AD∥BC
∴=
=
②连接AO，设S△OEG=9a，
∵AD∥BC，
∴△OEG∽△OCB
∴S△OEG :S△OBC=9:25
∴S△OBC=25a
∵AE:EG=1:3
∴S△OAE : S△OEG=1:3
∴S△OAE =3a
∴S△OAG=12a
∵S△OAB : S△OAG=OB:OG=5:3
∴S△OAB=20a
∴S四ABOE=S△OAB+S△OAE =23a
∴S四ABOE : S△OBC=23a : 25a=23:25
练习册系列答案
相关题目
