题目内容
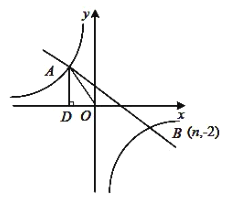
【题目】如图,⊙O中,弦CD与直径AB交于点H.若DH=CH=![]() ,BD=4,
,BD=4,
(1)AB的长为______.
(2)弧BD的长为________.

【答案】(1)8;(2)![]() .
.
【解析】
(1)根据垂径定理和勾股定理得出即可;根据勾股定理求出BH,根据勾股定理得出关于R的方程,求出R即可.
(1)连接OD,根据垂弦定理推论知道Rt△BHD中,BD=4,HD=![]() ,
,
由勾股定理得:BH=![]() =2
=2
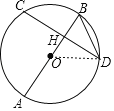
∵AB⊥CD,
∴∠BHD=90°,
设⊙O的半径为R,则AB=2R,OB=OD=R,
在Rt△OHD中,由勾股定理得:OH2+DH2=OD2,
即(R﹣1)2+(![]() )2=R2,
)2=R2,
解得:R=4,
∴AB=2×4=8.
故答案为:8.
(2)由(1)知道OB=OD=BD,所以弧BD所对的圆心角为60度,弧长为:
L=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目