题目内容
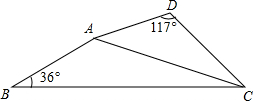如图，已知AD=3cm，AC=6cm，BC=9cm，∠B=36°，∠D=117°，△ABC∽△DAC．（1）求AB的长；（2）求∠BAD的大小．
解：（1）△ABC∽△DAC
∴∠DAC=∠B=36°，∠BAC=∠D=117°
AB：AD=AC：CD=BC：AC，
又AD=3，AC=6，BC=9，
∴AB=4.5cm．
（2）∠BAD=∠DAC+∠BAC=36°+117°=153°．
分析：（1）根据相似三角形的性质求出∠DAC和∠BAC的度数，找出对应边．然后根据已知边的长求出边AB和CD的长；
（2）然后根据相似三角形对应角相等，求出∠BAD的大小．
点评：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力，找准对应边及对应角是解决此类题目的关键．
∴∠DAC=∠B=36°，∠BAC=∠D=117°
AB：AD=AC：CD=BC：AC，
又AD=3，AC=6，BC=9，
∴AB=4.5cm．
（2）∠BAD=∠DAC+∠BAC=36°+117°=153°．
分析：（1）根据相似三角形的性质求出∠DAC和∠BAC的度数，找出对应边．然后根据已知边的长求出边AB和CD的长；
（2）然后根据相似三角形对应角相等，求出∠BAD的大小．
点评：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力，找准对应边及对应角是解决此类题目的关键．
练习册系列答案
相关题目
40、如图，已知AB∥CD，AB=3，BC=4，要使△ABC≌△CDA，则需（ ）
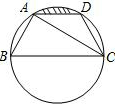如图，已知点A、B、C、D均在已知圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10cm．图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
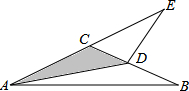（2013•定海区模拟）如图，已知△ABC中，∠CAB=∠B=30°，AB=
如图，已知，∠BAD=120°，AC平分∠BAD，若∠ABC+∠ADC=180°，则如下结论一定正确的有（ ）个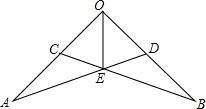
如图，已知C、D分别在OA、OB上，并且OA=OB，OC=OD，AD和BC相交于E，则图中全等三角形的对数是（ ）