题目内容
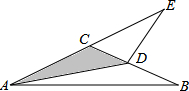 (2013•定海区模拟)如图,已知△ABC中,∠CAB=∠B=30°,AB=2
(2013•定海区模拟)如图,已知△ABC中,∠CAB=∠B=30°,AB=2| 3 |
分析:作CF⊥AB于点F,利用三线合一定理即可求得BF的长,然后证明△CDE是直角三角形,BD=x,则CD=DE=2-x,利用三角函数即可得到关于x的方程,解方程即可求解.
解答: 解:作CF⊥AB于点F.
解:作CF⊥AB于点F.
∵∠CAB=∠B
∴AC=BC,
∴BF=
AB=
,
在直角△BCF中,BC=
=2,
在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,
∴∠CDE=90°,
设BD=x,则CD=DE=2-x,
在直角△CDE中,tanE=
=
=tan30°=
,
解得:x=3-
.
故选B.
 解:作CF⊥AB于点F.
解:作CF⊥AB于点F.∵∠CAB=∠B
∴AC=BC,
∴BF=
| 1 |
| 2 |
| 3 |
在直角△BCF中,BC=
| BF |
| cosB |
在△CDE中,∠E=∠B=30°,∠ECD=∠CAB+∠B=60°,DE=BD,
∴∠CDE=90°,
设BD=x,则CD=DE=2-x,
在直角△CDE中,tanE=
| CD |
| DE |
| 2-x |
| x |
| ||
| 3 |
解得:x=3-
| 3 |
故选B.
点评:本题考查了图形的折叠,以及三线合一定理、三角函数,正确理解折叠的性质,找出图形中相等的线段、相等的角是关键.

练习册系列答案
相关题目
 (2013•定海区模拟)如图,已知Rt△ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )
(2013•定海区模拟)如图,已知Rt△ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D5,…,Dn,分别记△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面积为S1,S2,S3,…Sn.则Sn为( )