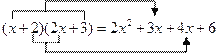题目内容
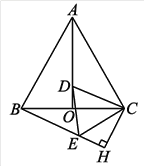
【题目】已知O为直线AB上一点,射线OD、OC、OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=50°,设∠BOE=![]()
(1)若射线OE在∠BOC的内部(如图所示):
①若![]() =43°,求∠COD的度数;
=43°,求∠COD的度数;
②当∠AOD=3∠COE时,求∠COD的度数;
(2)若射线OE恰为图中某一个角(小于180°)的角平分线,试求![]() 的值.
的值.

【答案】(1)①33°②15°
(2)n的值为30°或50°或110°或120°
【解析】
(1)①根据已知条件,可先求出∠COE,再根据角的差求出∠COD
②分两种情况讨论:当OD在∠BOC之间时;OD在∠AOC内的情况
(2)分四种情况讨论:当OE分别是∠BOC、∠BOD、∠COD、∠COA的角平分线时,根据角平分线的性质分别求出即可
(1)①∵∠BOC=180°∠AOC,∠AOC=120°
∴∠BOC=180°120°=60°
∵∠COE=∠BOC∠BOE,∠BOE=n=43°
∠COD=∠DOE∠COE,∠DOE=50°
∴∠COD=50°(60°43°)=33°
②当∠DOE在∠BOC之间时,设∠COD=x,则由题意可得:120+x=3(50+x)无解;
当OD在∠AOC之间时,设∠COD=x,则由题意可得120-x=3(50-x)解得x=15°
所以当∠AOD=3∠COE时,∠COD=15°
(2)如图: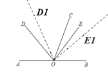
当OE1平分∠BOC时,
∵∠AOC=120°
∴∠BOC=180°120°=60°
∴n=∠BOE1= ∠BOC=30°;
如图: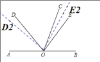
当OE2平分∠BOD2时,
n=∠BOE2=∠D2OE=50°;
如图: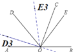
当OE3平分∠COD3时,
∵∠E3OC=∠D3OE3=50°,∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE3=∠BOC+∠E3OC=60°+50°=110°;
如图: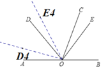
当OE4平分∠AOC时,
∵∠COE4= ∠AOC= ×120°=60°
∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE4=∠BOC+∠COE4=60°+60°=120°