Question

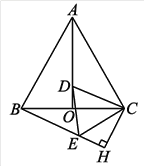
【题目】在等边△ABC中，AO是高，D为AO上一点，以CD为一边，在CD下方作等边△CDE，连接BE．

（1）求证：AD=BE；

（2）过点C作CH⊥BE，交BE的延长线于H，若BC=8，求CH的长．

Answer 1

【答案】（1）答案见解析；（2）4

【解析】

（1）先根据等边三角形的性质得出∠ACB=60°，∠DCE=60°，故可得出∠ACD=∠BCE，再由SAS定理即可得出△ACD△BCE即可得出AD=BE；（2）先由等边三角形三线合一的性质得出∠CAD的度数，再由△ACD≌△BCE得出∠CAD=∠CBE，再根据直角三角形的性质即可得出结论．

(1)证明：∵△ABC和△CDE都是等边三角形，

∴CA=CB,CD=CE,∠ACB=60,∠DCE=60，

∴∠ACD+∠BCD=∠ACB=60,∠BCE+∠BCD=∠DCE=60，

∴∠ACD=∠BCE.

在△ACD和△BCE中，

，

∴△ACD≌△BCE(SAS)

∴AD=BE；

(2)∵△ABC是等边三角形，AO是BC边上的高，

∴∠BAC=60，且AO平分∠BAC，

∴∠CAD=∠BAC=×60=30.

∵△ACD≌△BCE，

∴∠CAD=∠CBE，

∴∠CBE=30.

又∵CH⊥BE，BC=8，

∴在Rt△BCH中,CH=BC=×8=4，即CH=4.