题目内容
(2012•澄海区模拟)如图,在某海域内有三个港口P、M、N.港口M在港口P的南偏东60°的方向上,港口N在港口M的正西方向上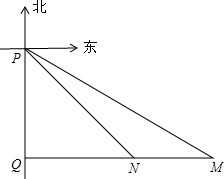 ,P、M两港口相距20海里,P、N两港口相距10
,P、M两港口相距20海里,P、N两港口相距10
海里.求:
(1)港口N在港口P的什么方向上?请说明理由;
(2)M、N两港口的距离(结果保留根号).
 ,P、M两港口相距20海里,P、N两港口相距10
,P、M两港口相距20海里,P、N两港口相距10| 2 |
(1)港口N在港口P的什么方向上?请说明理由;
(2)M、N两港口的距离(结果保留根号).
分析:(1)在Rt△PQM中,由∠MPQ=60°可知∠PMQ=30°,再根据PM=20海里,可知PQ=
PM=10海里,在Rt△PQN中,利用锐角三角函数的定义即可得出∠QPN的度数;
(2)由(1)可知Rt△PQM为等腰直角三角形,故NQ=PQ,在Rt△PQM中,利用MQ=PQ•tan∠QPM可求出MQ的长,再由MN=MQ-NQ即可得出结论.
| 1 |
| 2 |
(2)由(1)可知Rt△PQM为等腰直角三角形,故NQ=PQ,在Rt△PQM中,利用MQ=PQ•tan∠QPM可求出MQ的长,再由MN=MQ-NQ即可得出结论.
解答:解:(1)在Rt△PQM中,
∵∠MPQ=60°,
∴∠PMQ=30°,
又∵PM=20,
∴PQ=
PM=10(海里),
在Rt△PQN中,cos∠QPN=
=
=
,
∴∠QPN=45°.
答:港口N在港口P的东南方向(或南偏东45°);
(2)由(1)可知Rt△PQM为等腰直角三角形,
∴NQ=PQ=10(海里),
在Rt△PQM中,
∵MQ=PQ•tan∠QPM=10×tan60°=10
(海里),
∴MN=MQ-NQ=(10
-10)海里.
答:M、N两港口的距离为(10
-10)海里.
∵∠MPQ=60°,
∴∠PMQ=30°,
又∵PM=20,
∴PQ=
| 1 |
| 2 |
在Rt△PQN中,cos∠QPN=
| PQ |
| PN |
| 10 | ||
10
|
| ||
| 2 |
∴∠QPN=45°.
答:港口N在港口P的东南方向(或南偏东45°);
(2)由(1)可知Rt△PQM为等腰直角三角形,
∴NQ=PQ=10(海里),
在Rt△PQM中,
∵MQ=PQ•tan∠QPM=10×tan60°=10
| 3 |
∴MN=MQ-NQ=(10
| 3 |
答:M、N两港口的距离为(10
| 3 |
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意找出对应的直角三角形,利用锐角三角函数的定义得出结论是解答此题的关键.

练习册系列答案
相关题目
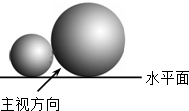 (2012•澄海区模拟)两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( )
(2012•澄海区模拟)两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( )