题目内容
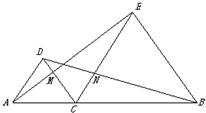
 19、如图,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N.
19、如图,△DAC和△EBC都是等边三角形,AE,BD分别与CD,CE交于点M,N.(1)证明:△ACE≌△DCB.
(2)在两组线段:①CM与CN;②AC与DN中,有相等的线段吗?
(只须写出结论,不须证明)
分析:(1)根据等边三角形的性质可知AC=DC,CE=CB,由∠ACE=60°+∠DCE,∠DCE=60°+∠DCE可得∠ACE=∠DCB,根据全等三角形的判定SAS可证得△ACE≌△DCB;
(2)根据全等三角形全等的判定可证得△ACM≌△DCN,即可得CM=CN,AM=DN.
(2)根据全等三角形全等的判定可证得△ACM≌△DCN,即可得CM=CN,AM=DN.
解答:解:(1)在△ACE和△DCB中,
∵AC=DC,CE=CB,(等边三角形)
又∠ACE=60°+∠DCE,∠DCE=60°+∠DCE即∠ACE=∠DCB,
∴△ACE≌△DCB(SAS);(8分)
(2)相等的线段只有CM=CN.(2分)

∵AC=DC,CE=CB,(等边三角形)
又∠ACE=60°+∠DCE,∠DCE=60°+∠DCE即∠ACE=∠DCB,
∴△ACE≌△DCB(SAS);(8分)
(2)相等的线段只有CM=CN.(2分)
点评:本题主要考查了全等三角形的判定的性质,涉及到全等三角形的性质,熟练掌握全等三角形全等的判定是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 21、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有
21、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有 8、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN.其中,正确结论的个数是( )
8、如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB; ②CM=CN;③AC=DN.其中,正确结论的个数是( )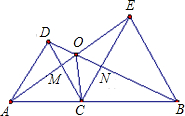 如图,△DAC和△EBC均为等边三角形,AE,BD交于O点,且分别与CD,CE交于M,N.则下列结论:①AE=BD;②CM=CN;③∠AOB=120°;④CO平分∠AOB.其中正确的有( )
如图,△DAC和△EBC均为等边三角形,AE,BD交于O点,且分别与CD,CE交于M,N.则下列结论:①AE=BD;②CM=CN;③∠AOB=120°;④CO平分∠AOB.其中正确的有( ) 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,结论正确的有
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,结论正确的有