题目内容
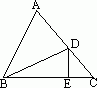
已知:如图所示,△ABC中,BD是角平分线,DE⊥BC,E为垂足,且AB=18cm,BC=12cm,S△ABC=90cm2,求DE的长.
答案:
解析:
提示:
解析:
|
解:过点D作DF⊥AB于F ∵DE⊥BC,∴∠BED=∠BFE= ∵BD是角平分线,∴∠ABD=∠CBD. 在△DBE和△DBF中, ∴△DBE≌△DBF.∴DE=DF ∵S△ABC=S△ABD+S△BCD=90cm2,AB=18cm,BC=12cm ∴ 即 ∴DE=6cm 即DE的长为6cm.
|
提示:
|
提示:本题用到分割后三角形的面积和等于原三角形的面积. |

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
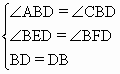
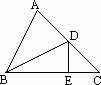
 7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( )
7、已知:如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判定a∥b的是( ) 已知,如图所示,Rt△ABC的周长为4+2
已知,如图所示,Rt△ABC的周长为4+2 22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由.
22、已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE∥DB,交AB的延长线于点E,AC与CE相等吗?请说明理由. 24、已知:如图所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
24、已知:如图所示,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由. 已知:如图所示,正比例函数y=ax的图象与反比例函数y=
已知:如图所示,正比例函数y=ax的图象与反比例函数y=