题目内容
22、已知：如图所示，四边形ABCD是矩形，对角线AC，BD相交于点O，CE∥DB，交AB的延长线于点E，AC与CE相等吗？请说明理由．分析：根据BD∥CE，CD∥BE即可证明四边形BECD为平行四边形，即BD=CE，又∵矩形对角线相等，∴AC=BD=CE．
解答：解：相等．
证明：∵BD∥CE，CD∥BE，
∴四边形BECD为平行四边形，
∴BD=CE，
又∵矩形对角线相等，即AC=BD，
∴AC=CE．
证明：∵BD∥CE，CD∥BE，
∴四边形BECD为平行四边形，
∴BD=CE，
又∵矩形对角线相等，即AC=BD，
∴AC=CE．
点评：本题考查了平行四边形的判定，平行四边形对边相等的性质，矩形对角线相等的性质，本题中求证BD=CE是解题的关键．
练习册系列答案
相关题目
小明将一副三角板按如图所示摆放在一起，发现只要知道AB，BD，DC，CA四边中的其中一边的长就可以求出其他各边的长，若已知AB=2，则CD的长为
，求这块铁片的长和宽．
，求这块铁片的长和宽．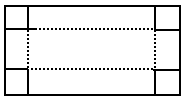
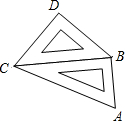小明将一副三角板按如图所示摆放在一起，发现只要知道AB，BD，DC，CA四边中的其中一边的长就可以求出其他各边的长，若已知AB=2，则CD的长为________．
的图象与
轴相交于点
，点
在该抛物线图象上，且以
为直径的⊙
恰好经过顶点
.
的值;
的坐标；
的纵坐标为
，且点
上运动，试探索：
时，求
为△
的面积，
为△
的面积，
为四边