题目内容
将一次函数y=x图象向下平移b个单位,与双曲线y=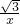 交于点A,与x轴交于点B,则OA2-OB2=
交于点A,与x轴交于点B,则OA2-OB2=
- A.
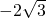
- B.

- C.
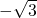
- D.

B
分析:平移后解析式是y=x+b,代入y=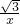 求出x2+bx=
求出x2+bx= ,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x+b)2-b2=2(x2+xb),代入求出即可.
,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x+b)2-b2=2(x2+xb),代入求出即可.
解答:∵平移后解析式是y=x+b,
代入y=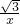 得:x+b=
得:x+b=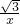 ,
,
即x2+bx= ,
,
y=x+b与x轴交点B的坐标是(-b,0),
设A的坐标是(x,y),
∴OA2-OB2
=x2+y2+(-b)2
=x2+(x+b)2-b2
=2x2+2xb
=2(x2+xb)
=2×
=2 ,
,
故选B.
点评:本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.
分析:平移后解析式是y=x+b,代入y=
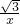 求出x2+bx=
求出x2+bx= ,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x+b)2-b2=2(x2+xb),代入求出即可.
,y=x+b与x轴交点B的坐标是(-b,0),设A的坐标是(x,y),求出OA2-OB2=x2+(x+b)2-b2=2(x2+xb),代入求出即可.解答:∵平移后解析式是y=x+b,
代入y=
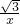 得:x+b=
得:x+b=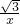 ,
,即x2+bx=
 ,
,y=x+b与x轴交点B的坐标是(-b,0),
设A的坐标是(x,y),
∴OA2-OB2
=x2+y2+(-b)2
=x2+(x+b)2-b2
=2x2+2xb
=2(x2+xb)
=2×

=2
 ,
,故选B.
点评:本题考查了一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力的能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目