题目内容
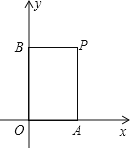
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点。例如,图中过点p分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB的周长与面积相等,则点p是和谐点。
判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
若和谐点P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
【答案】(1)∵点M不是和谐点,点N是和谐点;(2)a=6,b=9或a= -6,b= -3.
【解析】(1)根据和谐点的定义,利用矩形的面积和周长公式进行证明即可;
(2)当a>0时,根据(a+3)×2=3a,求出a,进一步求出b;当a<0时,根据(-a+3)×2=-3a,求出a,进一步求出b.
解:(1)∵1×2≠2(1+2),4×4=2×(4+4),
∴点M不是和谐点,点N是和谐点.
(2)由题意得,①当a>0时,(a+3)×2=3a,
∴a=6,
∴P(6,3),
∵点P在直线y=-x+b上,
∴代入得3=-6+b,
解得,b=9.
②当a<0时, (-a+3)×2=-3a,
∴a=-6,
点P(a,3)在直线y=-x+b上,代入得:b=-3,
∴a=6,b=9或a= -6,b= -3.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目