题目内容
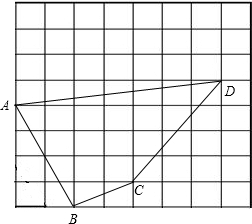 如图,每个小正方形的边长为1.
如图,每个小正方形的边长为1.(1)求四边形ABCD的面积和周长;
(2)∠ACD是直角吗?
分析:首先根据勾股定理求得AB、BC、CD、DA、AC的长,判断∠ABC和∠ACD是直角.即可求解.
解答:解:根据勾股定理得到:AD=
=
=5
;AB=
=
=2
;CD=
=5;BC=
=
.
AC=
=5.
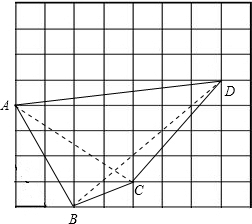
∴四边形ABCD的周长是:AB+BC+CD+AD=5
+2
+
+5=5
+3
+5;
∵(2
)2+(
)2=52,52+52=(5
)2.
∴BC2+AB2=AC2,AC2+CD2=AD2.
∴∠ABC和∠ACD是直角.
∴四边形ABCD的面积=直角△ABC的面积+直角△ACD的面积=
BC•AB+
AC•CD=17.5.
| 72+12 |
| 50 |
| 2 |
| 22+42 |
| 20 |
| 5 |
| 32+42 |
| 12+22 |
| 5 |
AC=
| 42+32 |

∴四边形ABCD的周长是:AB+BC+CD+AD=5
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
∵(2
| 5 |
| 5 |
| 2 |
∴BC2+AB2=AC2,AC2+CD2=AD2.
∴∠ABC和∠ACD是直角.
∴四边形ABCD的面积=直角△ABC的面积+直角△ACD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要运用勾股定理的逆定理,正确判断∠ABC和∠ACD是直角.是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 23、如图,每个小正方形的边长为单位长度1.
23、如图,每个小正方形的边长为单位长度1.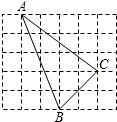 如图,每个小正方形的边长为1,则△ABC的面积等于
如图,每个小正方形的边长为1,则△ABC的面积等于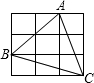 如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为
如图,每个小正方形的边长为1,以C为圆心3为半径的圆与AB的位置关系为 如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是
如图,每个小正方形的边长为1cm,蚂蚁从A点沿正方形的网格线,经过C点,爬到B点的最短路程是