题目内容
【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 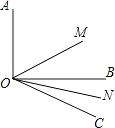
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
【答案】
(1)解:∠AOB=90°,∠BOC=30°,
∴∠AOC=90°+30=120°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=60°﹣15°=45°
(2)解:∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+15°,∠CON=
α+15°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() α+15°﹣15°=
α+15°﹣15°= ![]() α
α
(3)解:∠AOB=90°,∠BOC=β,
∴∠AOC=β+90°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() β+45°,∠CON=
β+45°,∠CON= ![]() ∠BOC=
∠BOC= ![]() β.
β.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() β+45°﹣
β+45°﹣ ![]() β=45°
β=45°
(4)解:根据(1)、(2)、(3)可知∠MON= ![]() ∠BOC,与∠BOC的大小无关
∠BOC,与∠BOC的大小无关
【解析】(1)先求得∠AOC的度数,然后由角平分线的定义可知∠MOC=60°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(2)先求得∠AOC=α+30°,由角平分线的定义可知∠MOC= ![]() α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC=
α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC= ![]() β+15°,∠CON=
β+15°,∠CON= ![]() β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】将正整数依次按如表规律排成4列,根据表中的排列规律,数2018应在( )
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 2 | 3 | |
第2行 | 6 | 5 | 4 | |
第3行 | 7 | 8 | 9 | |
第4行 | 12 | 11 | 10 | |
… |
A. 第672行第2列 B. 第672行第3列
C. 第673行第2列 D. 第673行第3列