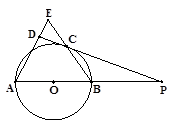题目内容
如图，PA 为⊙O的切线，B、D为⊙O上的两点，如果∠APB=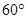
，∠ADB=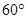.（１）试判断直线PB与⊙O的位置关系，并说明理由；（２）如果D点是优弧AB上的一个动点，当
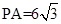且四边形ADBP是菱形时，求扇形OAMD的面积.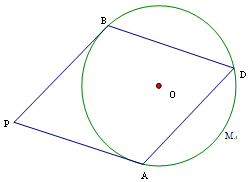
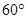，∠ADB=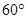.（１）试判断直线PB与⊙O的位置关系，并说明理由；（２）如果D点是优弧AB上的一个动点，当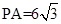且四边形ADBP是菱形时，求扇形OAMD的面积.⑴相切，理由：略⑵24π；
⑴连接OA,OB,通过四边形AOBP的内角和求得∠PBO=90°，得出结论
⑵连接OP,利用勾股定理求出OA长，即r, 连接OD ,求得∠AOD,在根据扇形面积公式求得
⑵连接OP,利用勾股定理求出OA长，即r, 连接OD ,求得∠AOD,在根据扇形面积公式求得
练习册系列答案
阅读快车系列答案
相关题目
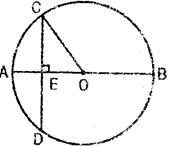
，BF＝3，求⊙O的半径长.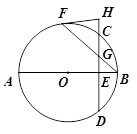
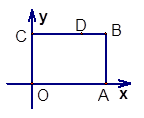
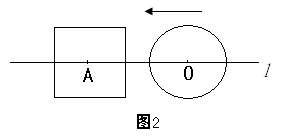
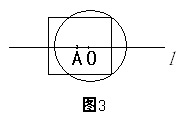
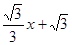与x轴、y轴分别相交于A、B两点，圆心P的坐标为（1，0），⊙P与y轴相切于点O，若将⊙P沿x轴向左平平移，当⊙P向左平移 个单位长度时，⊙P与该直线相切．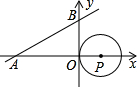 
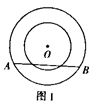
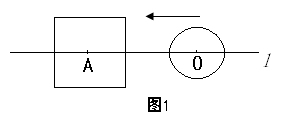
(2)若圆的半径为1，△ABE是等边三角形，求BP的长．