题目内容
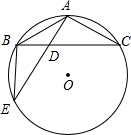（2002•岳阳）已知：如图，△ABC内接于⊙O，AB=AC=2| 3 |
分析：首先利用等边对等角与圆周角定理，证得∠ABC=∠E，则可证得△BAD∽△EAB，然后由相似三角形的对应边成比例，即可求得AE的长，继而求得线段DE的长．
解答：解：∵AB=AC，
∴∠ABC=∠C，
∵∠E=∠C，
∴∠ABC=∠E，
∵∠BAD=∠EAB，
∴△BAD∽△EAB，
∴AB：AE=AD：AB，
∴AE=
，
∵AB=AC=2
cm，AD=2cm，
∴AE=6cm，
∴DE=AE-AD=6-2=4（cm）．
∴∠ABC=∠C，
∵∠E=∠C，
∴∠ABC=∠E，
∵∠BAD=∠EAB，
∴△BAD∽△EAB，
∴AB：AE=AD：AB，
∴AE=
| AB2 |
| AD |
∵AB=AC=2
| 3 |
∴AE=6cm，
∴DE=AE-AD=6-2=4（cm）．
点评：此题考查了圆周角定理、等腰三角形的性质与相似三角形的判定与性质．此题难度适中，注意数形结合思想的应用．
练习册系列答案
相关题目
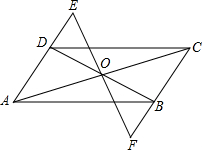（2002•岳阳）如图，已知?ABCD的对角线AC、BD相交于点O，过点O任作一直线分别交AD、CB的延长线于E、F，求证：OE=OF．
交于点G，垂足分别是E、F，AC是⊙O的弦，
AB=2，又关于x的方程x2-（b+2ac）x+m=0（m＜0）的两个实数根互为相反数．